物性の議論をするときにまず基本的に必要となってくるのは実際のバンド構造(Band Structure)がどのようになっているのかを示すことにある。
これによって、物質が半導体なのか金属なのかということを議論できたり、電気的、磁気的または光学的性質をこれで表してくれる(これは言い過ぎた、がまんざら嘘でもない。)。
しかしこのバンド構造をきちんとわかるには昔からいろいろな手段がとられてきたし、一筋縄では理解できないのが、問題である。(このことは今後、固体物理のほうできちんと扱っていこうと思う。)
バンド構造を知るときに、よく使われる手法が今から概論だけではあるが説明するTight-Binding-Model(強束縛近似)と有効質量近似と呼ばれている理論を用いる。
前者のほうが大切なので上のことを簡単に数式を用いて説明する。(しかし、難しいのでさらっと読み流してくれ)
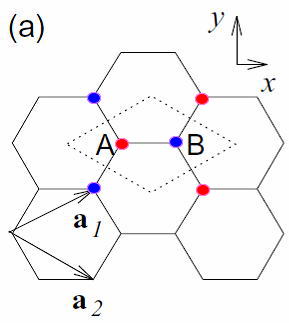
Tight-Binding-Modelとは、まずポテンシャルの対称性(ポテンシャルの対称とはCNTやグラファイトのように結晶自体に対称があるということ)と、一電子近似(実際の電子はたくさんの電子があるがそのうちの今回は炭素原子の一つのπ電子にだけ注目する。)をする。この条件のもと今回着目したπ電子の最近接原子にしか相互作用を受けない。今回のグラファイトなら3つの最近接原子がいる。
グラファイトの電子は一つの自由電子をもつが、量子力学で学習したように、この自由電子はπ電子(
)軌道に似た波動関数を持つが、結晶を考えるときにはこの固有関数はAとBのsiteにいるときで異なるので、今回はこの二つの固有関数を採用する。
今回のsiteA、Bの固有関数(左辺の波動関数)は以下のように書く、
は三つの原子の位置(A,Bの両方のそれに対応する原子を図にマークした)
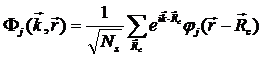
この波動関数は結晶の並進対称性よりBloch Function(ブロッホ関数)をとる。物性参照。
そして以下の関数を考える。
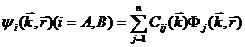
（nは単位胞内の原子軌道の数＝基底となるBloch関数の数）
i番目の固有エネルギー
は以下のように決定される。
；ハミルトニアン行列 
；重なり積分 
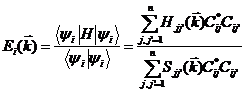
はエネルギーが最小になるように決定されるので、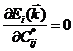
を計算すればよい。
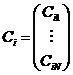を定義すれば
；トランスファー積分
；重なり積分
、
となり、
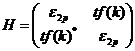であるので、上の行列式をそのまま解くと、
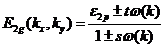
は
の軌道エネルギー。
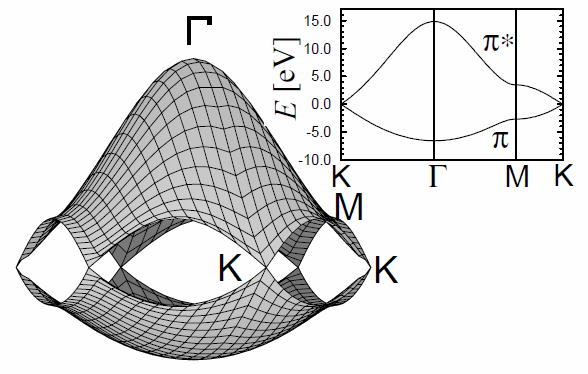
上半分が伝導帯、下半分が価電子帯になっており、逆格子空間上の点でこれら二つは接しているので、
ゼロギャップ半導体と呼ばれている。
以上でカーボンナノチューブを学ぶ上での下積みはすんだ。
