電力とエネルギー

　　　　　　　　　　　　　

素子に電流を流すと電圧の降下が起こる。つまり、ここで電子の流入がエネルギーの注入であり、

電圧降下によって、エネルギーが減っていることがわかる。

移動する電荷量は単位時間当たり　　i (t)

電圧　；　単位電荷を移動させるのに必要なエネルギー

よって、単位時間当たりのエネルギー　i (t)・v (t) [W]　ワット

電力量[J]≡[W・sec]

　　　　　　　　　　　　　　＝∫i (t)・v (t)dt


抵抗が使う消費電力

抵抗での電力低下による消費電力を計算する。

抵抗でオームの法則に従う場合　；　v (t)=i (t)・R

電力 　W_R＝i (t)・v (t)＝R・i ²(t)＝ｖ ²(t)/R

この消費電力は熱エネルギーとなり抵抗を熱くする。


コンデンサーの蓄えるエネルギー

　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

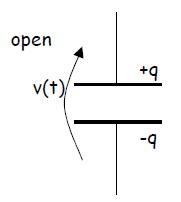
電荷が保存されており、電荷移動がゼロの回路がオープンな場合。

電流が流れず、外部電源との電流のやり取りがないために、

電圧があるが電力のやり取りはない。よって、消費電力はゼロである。

そこで、抵抗をつなげてやることで、蓄えられた電荷は電流として抵抗中を流れはじめる。つまり、

コンデンサー中に何らかのエネルギーが蓄えれていると考えられる。

　　　　　　　　　　　　　　　　　　　

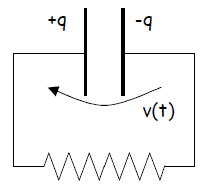
しかし、コンデンサーのエネルギーは先ほど考えられたような（一見そう思ってしまうが）

　　　　　　　　　　　　　　　　　　　　　　　　w (t)=q (t)・v (t)

ではない。

実は、この半分程度でのエネルギーで十分である。

なぜか・・・・・・定義に戻って考え直すと、

電荷と電圧の積であることには間違いないのであるが、電荷が増えていくにつれて電圧が

その電荷量によって徐々に変化するのがコンデンサーの性質であるからである。

　　　　　　　　　　　　　　　　　　　　　　　　q (t)=C・v (t)

よって、コンデンサーに q(t)だけ電荷を集めるのに必要なエネルギーは、

　　　　　　　　　　　　　　　　　

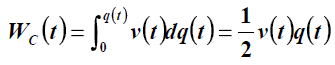
で計算される。