---

レリーフ型の回折レンズとは図に示したように　ｊ　番目のゾーンの回折光が１番目のゾーンの光に対し、
位相が波長の　ｊ　倍遅れて進行するようにゾーンの形状を構築し、さらに集光レンズの表面形状を
保っている。frenel zone plate方式と異なる点はゾーン内にも曲率をもたせることで、基準波λ0の
各ゾーンの１次回折光は、焦点方向に向かって球面波の一部として進行し、通常のレンズの透過波面と
等価な結像性能になる。



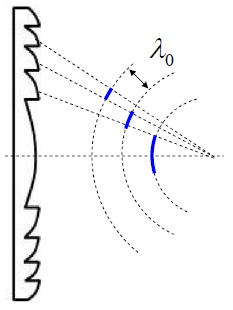
では、この回折レンズの効率はどの程度になるのだろうか？
このm番目からの波面の位相は、次の位相関数φを用いて表される。



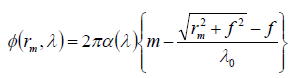
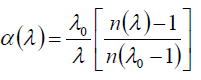
この式をフーリエ展開する。フーリエ展開する際に、透過光が f / j　の曲率半径をもつ球面波の集まりで
ある項で展開することにする。




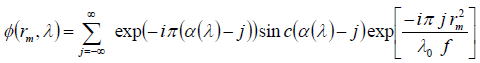
各項の絶対値の二乗



が f / j に集光する効率であり、例えば、回折レンズがfused silica(SiO2)で作られており、
Ｃ線（656.27nm)とＦ線（486.13nm）の中間波長で設計されているとした際に、
どのような回折効率になるかというと、



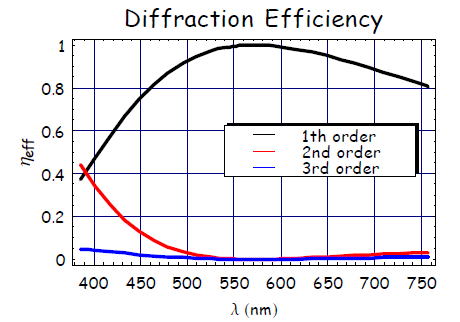
となり、設計した中間波長で１次の回折光の効率が１００％で回折光は効率が０％となるような
レンズを作製することが可能である。しかし、設計した波長からずれると回折効率は低下し、
いくつかの焦点を持つことになる。
カメラのレンズとして可視光領域をきちんと使えるようにするには積層型の回折レンズも考えられており
現在では、可視光領域では完全に１次回折光のみが焦点を持つレンズを作製することが
可能になっている。