Electron Density Dependence of the Excitonic Absorption Thresholds of GaAs Quantum Wells
phys. stat. sol. 2000 R.Kaur
1.Introduction
excitonとは電子と正孔(hole)の対となっているものである。Coulomb interactionでついになっているのであるが、これは明らかに水素原子の模型と似ている。つまり、エネルギー準位として水素のエネルギー準位のようなものを持っているということである。これらのexciton効果は二次元量子井戸の中で強められる。低温の中での量子井戸の吸収は1sのexcitonのためpeakは普通の吸収(continuum)と分裂して見られる。しかも他の2s,3sのなどや束縛のない伝導帯(continuum)からの吸収が見られる。
たとえばGaAsのようなものの場合1sのexcitonの束縛エネルギーは5〜15meVである。これは井戸の幅に依存する。
excitonの効果は密な電子gasが存在すれば頑固に存続することは知られている。量子井戸のinterband(バンド間)の遷移は吸収したフォトンのエネルギー近くに一つの閾値がある。フェルミエネルギー付近で励起された電子とホールはクーロン相互作用によって振動子強度を強め、その閾値の近くに弱いpeakが見られる。この弱いpeakはfermi edge singularityと呼ばれていて、金属のX線のスペクトルで見られる。(これに関しては他の論文で解説する。)
このほかにGaAs/AlGaAsの高移動度(電子が動きやすいということ)のトランジスターでは、電子が多少過剰にある状態で電子濃度をコントロールすることでいろいろな面白い光学特性が見られる。最近ではとても電子濃度の低い状態(1010cm-2)でexcitonのもう1つの状態が見つかった。これらはcharged excitonと呼ばれいて、excitonに1つの荷電子(正でも負の電荷でもよい)がついて計3つの複合状態(trion)である。余分な分の負の電荷がついたときには荷電励起子(X-)の余分な束縛エネルギーは典型的には1〜2meV(GaAs QWs)である。本論文では二次元電子系での荷電励起子の存在に関して述べた論文である。
introなので話がそれるがcombescotなどは金属でのX線領域のスペクトルを電子濃度の視点で議論している。適当な電子濃度では電子は二つの吸収閾値を持つ。これはholeが電子と束縛しているかしていないかによる状態の違いに対応している。二つの閾値のエネルギー差は束縛エネルギー(excitonの束縛エネルギーを振り払う分)とfemi energy分(電子が詰まっているところまで)の和である。この閾値はそれらの低エネルギー側でshake-up-process(機会があればそれに関して他の論文で述べる、簡単に言うと電子の内殻電子や中間殻電子が電離によってそれらの有効電荷が急激に変化するときに外側の電子がポテンシャルの変化を感じで励起準位へ遷移する過程。内殻、中間殻の電離はオージェ過程によって生じる電子が殻外へ遷移する過程はshake-off-processというこの過程の逆はshake-off-processという)によってtailを引くことが知られている。
Hawrylakは二次元電子系での励起子吸収スペクトルを計算した。Later Brown は荷電励起子の吸収スペクトルに関して計算した。このときは閾値は三つ存在する。荷電励起子と励起子と通常のfermi energyでの吸収とね。線幅は彼らのサンプルでは明確に分離することができなかったが、共鳴でのスペクトルの形は理論的なものと一致していた。
本論文では先ほども述べたように高純度で井戸から遠くにdopeした、gate電圧で電子濃度をコントロールしたGaAsの量子井戸のPLEスペクトルを報告する。light-holeとの発光を分離するために比較的狭い量子井戸を用いた。
2.Experimental Details
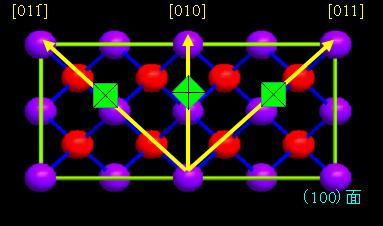
今回用いた試料はMBEでGaAsの基盤の(100)方向に結晶成長させたもので、100ÅのGaAsの量子井戸を扱った。1μmのGaAs、1μmのAlGaAs、0.5μmの超格子(複数の種類の結晶格子の重ね合わせにより、その周期構造が基本単位格子より長くなった結晶格子のこと。)GaAs(25Å)/AlGaAs(25Å)
、そのGaAsのQWは600ÅのundopedのAlGaAsのspacer、2000ÅAlGaAs(si-doped1017cm-3)そして170ÅのGaAsのcapをもちいた。sampleはFETのschotky contact と 井戸にOhmic contactで準備した。ohmic contactstとgateで電子を0〜3×1011cm-2まで井戸内の電子密度をコントロールできる。
3.Results and Discussion
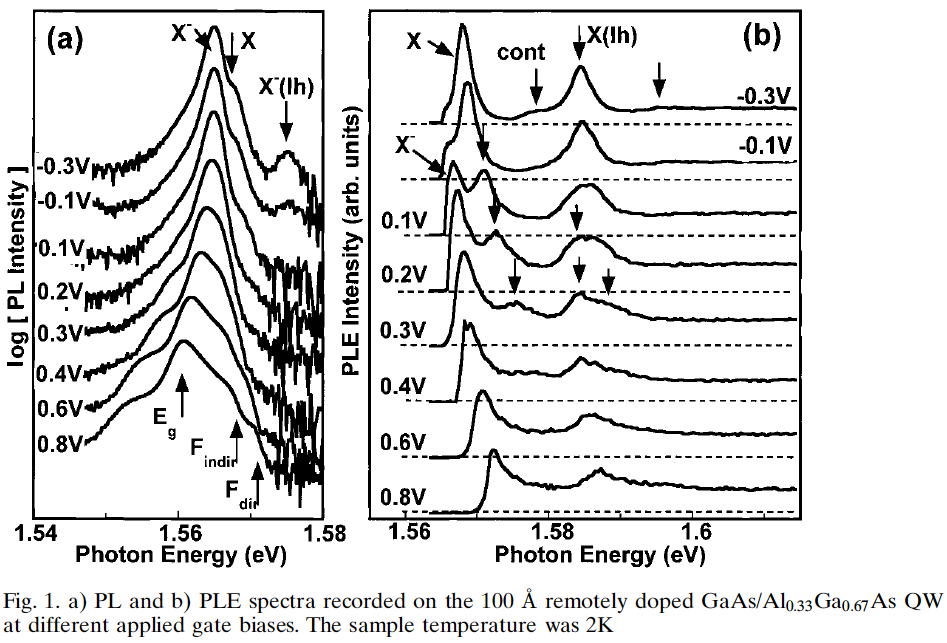
Fig1a.はgate電圧を変えて電子濃度を増加させて(上から下に)発光(PL)を取った。このdataはKuecherが比較的狭い井戸の2DEGsの発光と似ている。
発光がどこから起こっているのかを模式的に表すと、
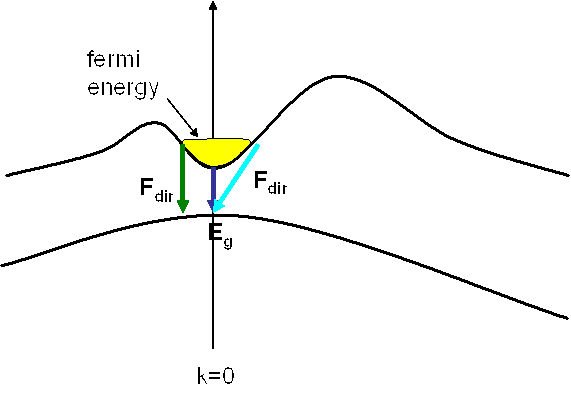
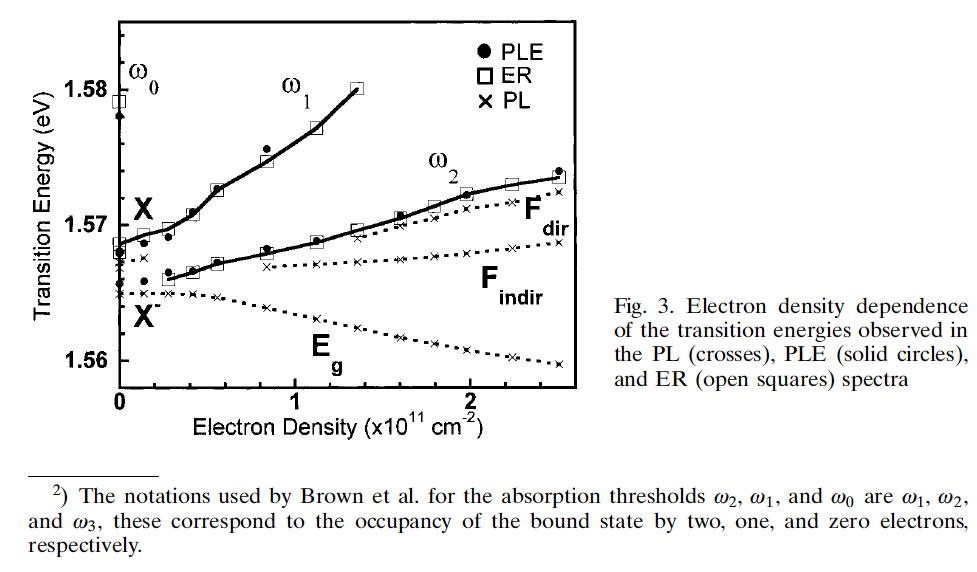
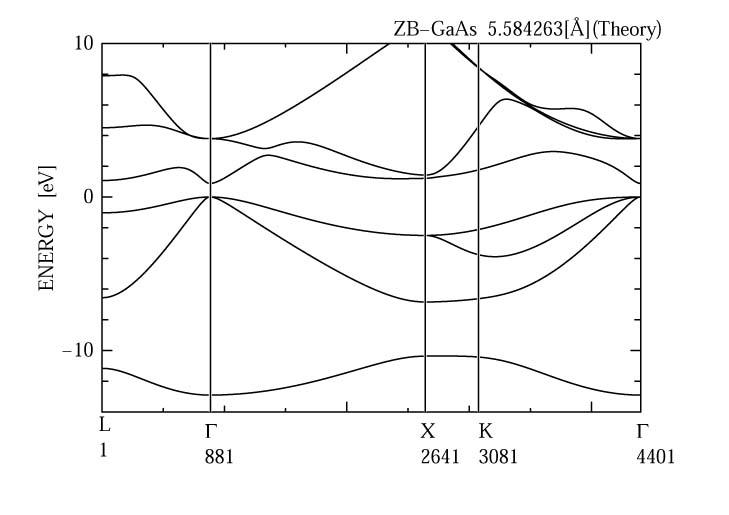
である。バンドギャップと間接遷移(indirect)の間の構造はshake-up-processによるものであるらしい。少し疑問になるのが間接遷移は発光しづらいのに間接遷移のほうが強く出ているのは何でであろう?hole側の受け入れ先が多くあるからか?indirect transitionのほうがdirectより低エネルギーにあるのは図を見ればわかるように価電子帯分のへこみ分だけエネルギーだけdirect transitionは高エネルギー側になる。
Fermi energyと電子密度はEgとFindirectの肩で概算している。
電子密度はcapacitanceの測定とよく一致した。
電圧を0.1Vとするとcharged excitonのsharpなものが見えたし、高エネルギー側にexcitonも出現した。charged exciton と excitonのエネルギー差は2.1meV。
電子を少なくするとfermi energyが下がるので発光は鋭くなる。PLもhigh energyのほうにshiftしている。これのあまり理由は和からない。
次にfig.1(b)のPLEに関して議論する。gate biasを-0.3Vとすると1sのheavy-holeのexciton(X)の発光とlight-holeのexciton(X(lh))の発光の両方が見られる。これらの発光は同じバイアスのエネルギーに似ている。(個人的にはほとんど(X)のほうは一致しているが、(Xlh)のほうはPLEのほうが高エネルギー側にあるように見えますが)
XやX(lh)のところにいくつがでこぼこが見られるが、それらは2s,3sなどのからの発光と束縛されていないところからの1sと2sのエネルギー差からheavy-hole excitonの束縛エネルギーは11.4meV考えられる。
gate biasが0.8VのときFermi-edge-singularityのために吸収の閾値でpeakが見られる。(どのことを言ってるんや)
あんまりこの時点でこの論文の言っている意味がわからない。というより、話に一貫性がないんじゃないんとおもう。そんなことより実験データのほうが興味深くはあるが、
Fig.1(b)はcharged-excitonとexcitonの発光が電子濃度を増加させるにつれて、強度が入れ替わっているのが興味深いやはり、電子濃度を増加させるにつれてcharged-excitonの強度が強くなってきている。このことはPLに関しても同様なことがいえる。
PLEで電子濃度を増加させるとpeakが高エネルギー側にshiftしているのがわかるしかもスムーズにFESのpeakにつながっている。
同時にexcitonのpeakは電子濃度が6×1010cm-2で見分けることが難しくなっている。
このような特徴はexcitoのlight-holeに関してもかなり電子濃度の関して似たような振る舞いになっている。