係丏侾丂丂娭悢娭學傪傕偮暔棟検偺娫偺岆嵎偺庢傝埖偄
椺偊偽捈曽懱嵽椏偺枾搙兿傪媮傔傞偙偲傪峫偊傞丅枾搙兿傪捈愙寁應偡傞偙偲偼擄偟偄偺偱埲壓偺峫嶡傪峴偆
幙検M丄奺曈偺挿偝倢倶丄倢倷丄倢倸偺娫偵偼丄
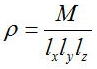
偙偙偐傜枾搙傪嶼弌偡傞応崌偵丄M傗倢倶摍傪寁應偡傞昁梫偑偁傞偑丄
偦偺嵺偵奺寁應寢壥偼岆嵎傪娷傓偙偲偵側傞丅
偦偆偟偨嵺偵丄枾搙兿偼偳偺傛偆側岆嵎偱婰弎偱偒傞偺偐峫嶡偟傛偆
乮侾乯侾曄悢偺応崌偺庢傝埖偄
師偺傛偆側侾曄悢A偺暔棟検Z乮A乯傪峫偊傞
偙偺偲偒嚈Z傪嚈A傪梡偄偰寁嶼偡傞偙偲傪峫偊傞
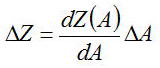
埲忋傪梡偄偰侾曄悢偺暔棟検A傪梡偄偰丄嵟廔揑側暔棟検嚈Z傪嶼弌偡傞偙偲偑壜擻偲側傞
乮俀乯懡曄悢偺応崌
懡曄悢偵側偭偨偲偟偰傕婎杮揑側偙偲偼曄傢傜側偄丅昁梫側偺偼扨弮側旝暘偺抦幆偩偗偱偁傞丅
Z乮A,B乯偵娭偟偰A,B偺暔棟検傪梡偄偰岆嵎検嚈Z傪埲壓偺傛偆偵寁嶼偡傞偙偲偑壜擻偱偁傞
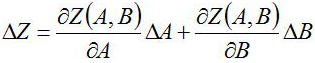
偝傜偵丄偙傟偺擇忔榓傪偲傞
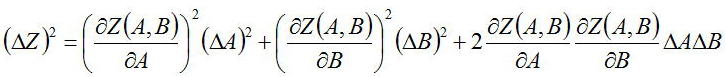
嚈Z丱俀偺偽傜偮偒偼丄暯嬒抣偺抣傪峫偊傞丅嚈A丱俀偲嚈B丱俀偼曄悢A偲B偺偽傜偮偒偺擇忔榓暯嬒抣
冃A丱俀偲冃B丱俀偱偁傞丅愭傎偳傕壗搙傕傗偭偰偒偨傛偆偵亙冃A冃B亜偼椉幰偼撈棫側偺偱
偦偺愊偺暯嬒偼侽偵側傞丅傛偭偰
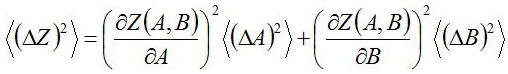
埲忋偐傜偽傜偮偒偺昡壙傕偡傞偙偲偑壜擻偱偁傞
偝傜偵峫偊傪恑傔傞偲堦斒揑偵曄悢傪憹傗偟偰媍榑偟偰傕慡偔曄傢傜側偄丅
