４．２　　最小二乗法

（１）問題提起

よく実験では二つの物理量の関係を明らかにするためにグラフを用いることが多々ある。

その際に ｙ＝ｆ（ｘ）　を決定することになるが何かいい決定方法があるのだろうか？



（２）最小二乗法

ｎ個の測定値（ｘ１、ｙ１）、（ｘ２、ｙ２）、・・・・・、（ｘｎ、ｙｎ）があるとする。

ここではｘ値に誤差がなく、ｙのみ誤差があるとする。

任意のｉ番目の測定値　ｙｉ　がある関数ｙ（ｘ）に従うとすると、誤差量は、



最良のｙ（ｘ）の形は何であろうかと考えた際に、最良の関数ｙ（ｘ）は各測定値からの誤差量の総和が

最小値になることである



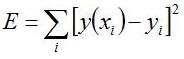
よって、これが最小二乗法と呼ばれるゆえんである

では、グラフに関数を描く際に、ある理論的根拠からｙとｘの間にはある関係式の関数を描きたいと思う。

例えばそれが直線；ｙ＝ａｘ＋ｂである場合、最良のａとｂを決定したい。

上式の最小二乗法の関数において、ｙ（ｘ）に含まれる決定したい係数がａ１、ａ２、・・・・・、ａｎだとすると

上式は次のように書き換えられる。



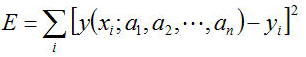
この係数ａ１、ａ２、・・・・・、ａｎは以下のようにｎ個の連立方程式を立てることで決定できる



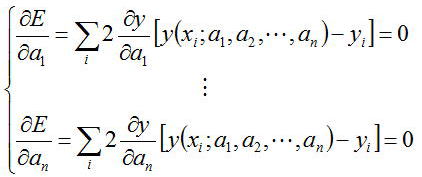
つまり、誤差量の総和Ｅがａ１、ａ２、・・・・・、ａｎが最良に選ばれていたとすると

各ａの係数を変化させてもＥが最小値ならばＥの変化量は０となるところから上式の連立方程式が導かれる

しかしながら注意しなければならないことは上式の連立方程式はＥが極小値をとっていても

成り立つという点である。つまりＥが最小値をとっていない可能性がある。

その際には連立方程式の解の組み合わせがいくつかあるので、

最小になるものを特定する作業をする必要がある