４．３　　誤差の重みづけ

測定結果に基づいて議論するわけだが、

その測定値がある重みがある時にはどのように考えればよいのだろうか？

その前に、測定値に重みがあるとはどういうことなのかを議論する。

（１）重みとは

１０回の測定を行い、ｘ１、・・・・・ｘｎまでの値を得て、これを二つのグループに分けて平均値（測定値）を算出する。



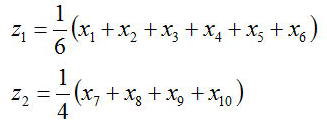
それぞれの平均値ｚ１とｚ２から、本来計算したい平均値＜ｚ＞は以下の式になる



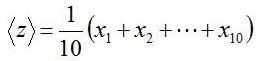
では、ｚ１とｚ２を用いてこの平均値を計算する際に、＜ｚ＞＝（ｚ１＋ｚ２）/２　さらに平均値をとるのではなく

以下のようにｚ１とｚ２にそれぞれ異なる重みをかけてやる必要がある



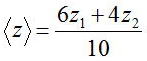
よって、一般的に重みｗ１、ｗ２、・・・・・、ｗｎを持つ数値の組みｚ１、ｚ２、・・・・・、ｚｎがある時

その最良の値は、



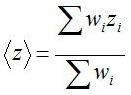
である。しかし、式では上記のように書けばいいが、どのように重みを決定すればいいのだろうか？

重みの決定方法は難しいので、また機会を見つけて記載したいと思う

ところで、最小二乗法においても各測定値（ｘｉ，ｙｉ）の重みがｗｉであったとすると、



となり、ここで使われているｙ（ｘ）を決定するために、各パラメータの偏微分０になるように

連立方程式を立ててｙ（ｘ）を決定する