オームの法則
電気回路において、ある電子素子(抵抗素子)は電圧と電流の関係が比例関係であることがある。
つまり、
v=iR
この関係は、直流電圧のときのみではなく、交流電圧のときでも成り立つ関係式である。
抵抗体は、その断面積Sと抵抗体の長さ l と比例定数(抵抗率ρ)で表現することができる。
実際、抵抗の長さが長ければ、それに比例して電流は流れにくく、また、断面積が大きいほど断面積に多く
の電子が含有するために、大電流が流れる。そのため、抵抗に反比例する。
R=ρl/S
オームの法則はもう1つの見方をするときがある。
i=v/R=Gv
と呼ばれる。比例定数G(コンダクタンス)と呼ばれているもので表現する方法である。
コンダクタンスの単位はジーメンス[S]であり、抵抗素子の電圧に対する電流の流れやすさである。
コンデンサ
次に、コンデンサに関して述べようと思う。コンデンサは電気回路によく用いられる回路素子である。
構造は、対向する2つの平行な電極板からなる構造で、その電極板に電圧Vをかけると静電誘導(導体に
帯電した物体を近づけると、導体に電荷分布が生じる。つまり、導体は、帯電した物体に近い側では、帯電し
た物体の異種の電荷が、遠い側では同種の電荷が生じる。)が生じ、電荷がたまる。
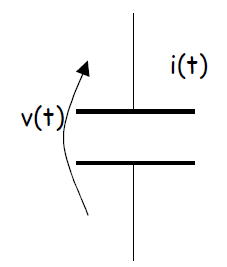
電磁気学の項目で述べたように、コンデンサは、集まる電荷qは電圧に比例する。その比例係数をC
(静電容量)とし、
q=CV
この比例定数の単位はF(ファラッド)である。Cは用いた電極板の形状と電極板間に挿入された誘電体の
性質によって異なる。また、電磁気の項目で述べたように電極間の距離dが短くなるほど、誘電体の誘電率
εが大きいほど、加えた電圧から生じる電界が強くなり、電荷を誘導するチカラが(電子をためるのに必要な
チカラのこと)が増加する。また、電極板の面積が大きいほど多くの電荷が集まる。だから、容量Cの間に
以下の関係式が成り立つ。
C=εS/d
となる。(より詳しい解説は電磁気学の項目にあるので見るとよい。この項目では電気回路であるので
必要以上の解説は行わない。)
ここで重要なことは、電気回路で考える際に、コンデンサにかかる電圧が時間的に変動しなかった場合は
コンデンサにたまっている電荷は変化しないことが上の式からわかる。つまり、コンデンサ周辺において
電流が流れていないことを示唆している。
では、次に時間的に電圧が変化した場合を考えてみよう。この際、上の式で静電容量は物質固有の
ものなので時間的に変化しないため、以下の式で考えることができる。
Δq=CΔV
つまり、コンデンサにためられた電荷は電圧がΔVだけ変化したことによって、Δqだけの電荷の変化を
受けたことを示している。この電荷の時間変化は電流が生じたと考えられる。
電流は、単位時間当たりの電荷の移動量であるからΔq/Δtで表現することが可能である。
時間を無限小にすると、
i=dq/dt=C・dV/dt
と表現される。
余談であるが、実際のコンデンサは時間がたつと電荷がもれて減っていくという好ましくない現象が起こるが
今回考えている理想的な回路素子はキャパシタといって、現実に近いコンデンサという呼び方とは
区別する場合があるので注意が必要である。
コイル
次に、これもまたよく使われる、電子回路素子の1つとしてコイルがある。
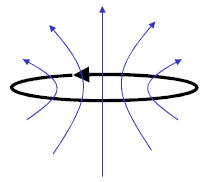
コイルは電流がそれに流れると磁束(磁場(磁束密度)、磁束とは磁力線の数、電磁気学参照)が発生し、
この磁束と巻線自身との鎖交磁束数Ψは電流 i に比例する。(理由は電磁気学に関して述べる)
つまり、
Ψ=L i
であり、Lはコイルの形状(面積S、長さl)
磁性体の透磁率 μ
総巻数 n
に依存する。
L=μn2S/l
となり、Lは自己インダクタンス[H];ヘンリー
コイルに電流を流すと、
H=n i/l ;磁界
φ=μHS ;磁束
Ψ=nφ=nμHS=i×μn2S/l ;交鎖磁束数
ここで、交流を変化させることを考えると、
磁束の変化 ⇒ 電磁誘導 ⇒ 誘導起電力
コイルの電圧Vは
V=dΨ/dt
であり、交鎖磁束数の時間変化に比例する。ことが知られている。
よって、
V=L di/dt
このような理想的な回路の場合実際のコイルという呼び方と区別し、インダクタと呼ばれている。
