方針

最終的な誤差にもっとも影響を及ぼす量を確認し、その量の測定を繰り返すか、異なる方法を用いるなどして、
誤差への影響の大きい量をできる限り低減する

	大課題	小課題	対策
�@	・効率よく目標とする物理量を評価したい （無駄な桁までの計算/すべての要素に対する計算の除去）	誤差のターゲット設定／必要精度	以前の節で述べたように誤差を測定値から推定する際に、測定回数ｎによるが誤差の誤差がある以上１／４よりよい精度で誤差を評価して用いる必要はない
�A		どの程度誤差なら無視してもよいか	（例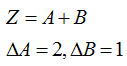） 　を例として考える Aの誤差のみを扱ったとしても１／８程度の差しか現れない。 もちろんA,B,C,D,・・・・と誤差要因が多くなった場合、無視した誤差が積算されるため、きちんと考慮に入れないといけないが、明らかに�傳が�僊の１／３以下ならばほぼ無視しても１ケタ程度小さくなるため無視しても問題はならないだろう そもそも�@にあるように１／４程度は誤差をもつものであるので、 それ以上きちんと誤差を算出する必要はない
�B		問題ない誤差をどこまで正確に計算すべきか	もしある量があまり影響を与えないと考えられる場合、誤差の値を高めに見積もっている限り大まかに扱っておけばよい。つまり、大きく見積もっていても誤差量に影響を与えないのため、上記のような考え方が可能になる
�C		複雑な関数の扱い方	評価したい測定量とその誤差が以下の関係式を満たすものとする 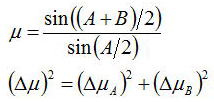上式から誤差を計算する際に元の式を偏微分して、AとBの平均値＜A＞と＜B＞を代入する必要がある。しかし、複雑な計算になるほど計算間違えが起こる可能性もあり、もっと簡単に計算する方法が必要である。 そのためには、以下の計算を行えば、完全に一致することはないにしても誤差を扱ううえでは問題ないレベルで一致するはずである。 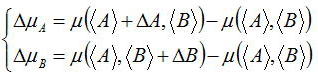�僊と�傳は測定量AとBの標準誤差を与えればよい
�D	・系統誤差の扱い方	系統誤差が小さくない場合の扱い方	まず、何らかの形で系統誤差を決めて取り除くことによって、残りの誤差はをランダムで独立である（偶然誤差）であると考えることができる。 これによって、おおよその系統誤差量と偶然誤差量の程度が判断可能である
�E		最終的な誤差量	最終的な誤差量の必要条件 �@系統誤差は可能な限り取り除かれている �A偶然誤差は適当な統計的方法により見積もられている �B他の重要でない誤差は少し高めに見積もられており、無視できる量である �Cいくつかの要素による誤差の合算を行っている ⇒�Cで算出した誤差量は、もし、同様の環境で実験を行った場合、再現性を持った結果が得られると考えてよい （やってはいけないこと） ・�@−�Cの後、不明な系統誤差があるかも知れないと考え、ある任意の因子だけの誤差を大きく見積もる誘惑に駆られるかもしれない このような主観的な誤差の過大評価をすることは絶対にやってはいけないことである
�F	・測定器の扱い方	測定器の分解能による誤差の考え方	Length(mm) 325 325 325 325.5 325 325 M + σm=325.08±0.0833 上記の表から標準誤差と平均値を算出した際に、上記になるが実際にこのような考え方で誤差を算出してもいいか？ 答えはNoである。理由は測定器の分解能が足りないからである。値が０．５ごとに丸め込まれており、これから言えることは、 M＋誤差＝325±0.5 or 0.25 ということだけである。 より詳しく知る必要があるならば、より高精度・高分解能の測定器を買うべきである
�G	・誤差算出上の注意事項	積や商が含まれる	数式に積や商が含まれる場合 以下のように誤差の割合が拡大してしまうことになる （例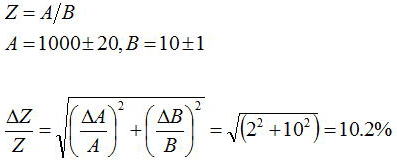） この式からわかるとおり１０％の誤差をさらに小さくしたい場合にはAの誤差を小さくするよりもBの誤差を小さくする方が得策であることが分かる。 つまり、実験を計画するさいにはもっとも誤差の影響が大きい要素をできるだけ小さくすることを考える
		差が含まれる	数式に近い値の差を考慮する場合 以下のように誤差の割合が拡大してしまうことに気を配る必要がある （例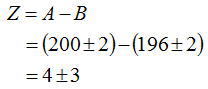） この結果をみると最終的に75％も誤差を含むことになる よってZを評価する上でほかの方法を考える必要があることが明らかである