分光器の分解能

実験

実験配置は変更せず光源にHeスペクトル管で587nm付近の波長で実験した。この波長を用いたのは、スペクトルがδ関数的で他の波長の光に影響されない(つまり、他の波長のスペクトルがない)からである。

  分解能とは

分解能とは装置の接近したスペクトル線を分離できる能力を表す量のことをいう。分解能の定義としては色々とある。例えば、レーリーの定義、アッベの定義などがあるが、今回の実験で用いたのはδ関数的な光源が最終的に検出器側ではどのくらい広がって観測されるのかを表す、全半値幅という量を用いて評価した。全半値幅とは最大値の半分の値を取るときにおけるスペクトルの広がりで表す。回折格子における分解能を考えるとき、以前求めた式

　　　を入射角は一定にすると、(つまり、gratingは回転させないで出射側のスリットにできる分散)

　　　で、これが回折格子の分散で波長が異なった光はだけ異なった回折角

を示すことになる。実際の分光装置では回折光と入射光の方向は一定に保ち、回折格子を回転させて波長を変化させる。回折格子の理論的分解能は

Resolution

　　　ここで、与えられたNは回折格子にきってある溝の数である。ここで興味深いこととしては、分解能は高次の光のほうがいいということである。後、gratingの溝の数が多ければ多いほど分解能は上がるが無限に溝の数を増やしていくと回折が起こらなくなるので分解能には、やはり限界がある。

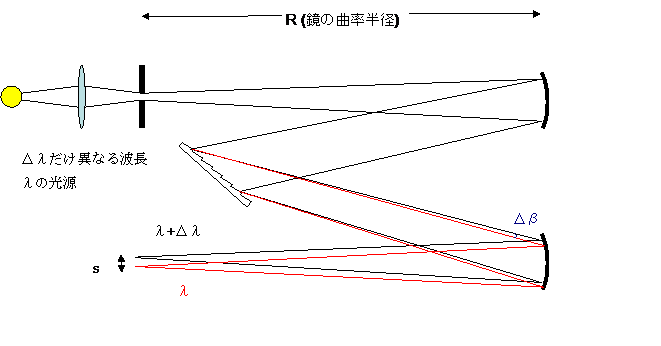
　上の図から凹面鏡の焦点距離がRであるので

　　　になる。(なぜこのようになるのか、gratingからmirrorまでのずれは考慮しないのか？とい
　　　う疑問をもたれる方がいると思うが、これに関してはレンズと同じようにこの凹面鏡を考え
　　　てみると、平行光がレンズに入射したときにレンズの中心を通るものを基準に考えてみれば
　　　理解できるだろう。)

　　　回折格子の場合は、

　　　であるから、スリット幅sに含まれるスペクトル幅は

　　　これが、分光器の分解能と考えることができる。波数幅で言うとの関係から

求まる。この式はs、つまりスリットの幅を小さくしていけばいくほど線形的に分解能は小さくなっていくことがわかる。しかし実際はそんなことはなく、回折格子の理論的分解能は上に述べたようにgratingの溝の数にも依存している。

　　　分光器が光学的に完全にできていると、実際の分解は上記のスリットの有限幅によるもの()と回折格子の理論的分解(s→0のときのdiffraction limit)によるもの(とする)決められる。これらの間には、

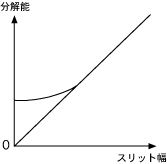
　　　の関係がある。つまり、スッリト幅を小さくしていくとgratingの溝の数に依存する分解能の限界を考慮していかないといけない。だからスリット幅に対して線型になることはない。右図のように曲線を描く。

今回の結果はgratingと出射側のスリット幅で分解能を記述したが、　　　　　　　　　　　　　　分光器には入射側のスリットもあり、これが分解能にどう影響を与えるのかも考える必要がある。入射側のスリットをあけると分光器の中にレンズで絞られていない光が入ってきてgratingに当たる光の中に平行光でない様な光が入ってきて分解能を下げる要因とはなる可能性はある。基本的にはレンズで絞られているはずだから入射側のスリットをあけておくことにそれほどメリットを感じない。では何のためにスリットをあけるのか？光をもっとスリットで絞りほとんど点光源にする必要はあるのか？この点に関しては疑問が残る。