2.2ブリュースター角

　　ブリュースター角について

フレネルの公式の特定の場合としてブリュースター角が導出させる。それなので、まずフレネルの公式について簡単に示しておく。(詳細はヘクト�T参照)。この式とスネルの公式から、反射係数の平行成分は0になる角度のときがある。この角度をブリュースター角といい、式は以下のようになる。

(ブリュースター角)

　　　　今回の実験はブリュースター角から実際何のガラスにレーザーを反射させていたのかを検証する。

実験配置図

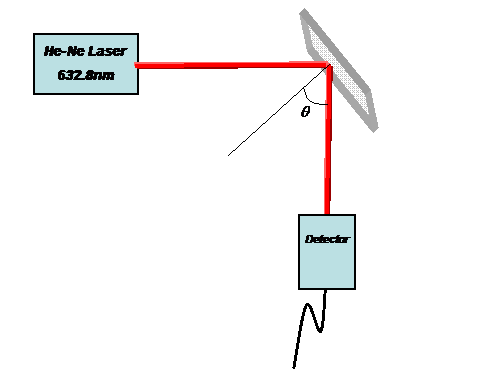
実験結果

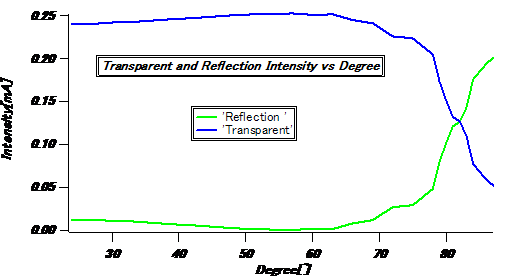
バックグラウンドは0.0001(mA)程度

全体強度→0.253mA

透過光強度＝全体強度−透過強度

この実験からブリュースター角は57度(角度で数度の誤差)であることがわかった。このときの屈折率は先ほどの式から1.5となりこれはガラスの屈折率とほとんど変わらない。

円偏光を用いた実験

偏光板に関する簡単な説明をする。

直線偏光板とはある特定方向のみの直線偏光を通過させることができる光学素子のことを言う。次にλ/4板に関してですが理想的には光量は変化させずに(実際は反射などがあるのでそんなことはないのだが)、結晶中で屈折率の違いから位相速度において高速軸と低速軸があり、相対的に高速軸のほうが位相でλ/4だけ速い状態が起こる光学素子である。円偏光板(無偏光をまたは直線偏光を円偏光に変える)はこれらの光学素子を組み合わせることで作られている。

円偏光板において注意しないといけないことがあり、使用の際に裏と表があるということで、その理由は円偏光板Aに関しては、たとえば、無偏光の光が右から入ってきたとするとλ/4板を通過した後は無偏光の光になっていて、次の直線偏光で直線偏光になって出てくる。結局、円偏光は形成されない。ところが円偏光板Bの右から光を入れたとするとまず直線偏光になりこれが、λ/4板の高速軸に対して45°傾くようにしておくそのときに低速軸のほうにλ/4の位相の遅れが生じ、合成したときに円偏光を生じさせる。

最後にガラスに関して述べる。ガラスによって反射された光は位相がπずれるということを習うが実際はそう単純でもない。ヘクトにも載っているのだが、反射後の位相変化は反射面に対して平行と垂直成分で振る舞いが異なる。大体ガラスならば空気からガラスで反射する際に、反射成分で反射面に対して垂直ならば、常に位相がπずれる。反射成分で反射面に対して平行成分ならブリュースター角までは位相がずれないが、それ以降は位相がπずれる。

　　実験配置図

　　　

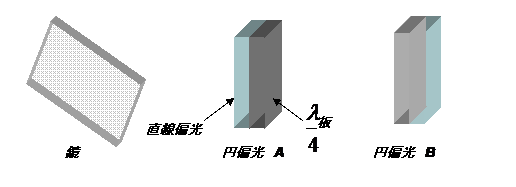
いずれも左から光を入射させる。

実験の前後で偏光板をA→Bへの交換は左右でひっくり返している。(上下でひっくり返してはいない)

実験結果

�A，�Bのとき理想的には、生光に関して50％が透過するが反射や吸収があるのでそれより小さい値になっている。二つの違いは�Aは円偏光が出ている。�Bは直線偏光が出てきている。

�Cに関しては、円偏光になり、それがまた円偏光になる。よって生光に対して光量は1/4になるが実際はそれより小さい。�Dは円偏光で1/2となり、また2枚目の直線偏光板では1枚目の偏光軸方向と同じ方向ならば理想的には変化しない。吸収などを考えると相対的には�Cの2倍になっているはずである。実験結果を見てみると�C、�Dはこの考察と同じ関係になっている。

�E、�Fの光量に関する考察も同じである。実験結果はやはり2倍の関係になっている。

�Gは鏡では理想的には光量は変化しなく位相だけを反転させるだけである。�Cと違うのは光の鏡による欠損だけである。�Hに関しては鏡によって位相がずれて右円偏光なら左円変更になるので最初の直線偏光軸と2枚目の直線偏光軸と直交するのでほとんど透過できない。

�I、�Jに関しても同じである。

　　　�Kは�Gと異なるのは2枚目の円偏光板Bのλ/4板が直前の直線偏光に対してきちんと45°差になっていない。そしてある程度円偏光板Bの直線偏光板で光がカットされている。よって、直線偏光板がどの程度回転されているかによって光量が変化する。