15世紀ごろ、ある問題が物理学者を悩ませた問題があった。
それは何かというと、長さ、おもりの質量が
の多くの単振り子を互いに固く連結させたとき、この全体の系はどのような長さの単振り子と等しい周期の振動を行うか
ということである。
まずこの問題を考える前に、以下の図のような剛体に関する、物理振り子の周期を求めて
見ることにしよう。
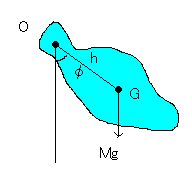
Oを水平軸、Gを重心として、
とする。重力MgのOの周りのモーメントを考えて、
これと単振り子の運動方程式（高校でもやりますよね）
と比べると（わからない人は下の記事を参照）
ならば、単振り子の運動方程式と一致する。
与えられた剛体の物理振り子は、上の条件を満たす長さを持つ単振り子と全く同じ
運動を行うことになる。このような単振り子を相等単振り子(equivalent simple pendulum)、
長さ l を相等単振り子の長さと呼ぶ。
小振動のときは簡単に周期を求めることでき、それは、
とし、
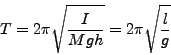
ほうほう、つまり、剛体の物理振り子に関しては、それに対応した単振り子が存在する
ってことですか。
この物理振り子の問題を最初に扱ったのは振り子時計を発明したことで名高い
Huygens（ホイヘンス）（高校物理をやったことがある人でこの人物を知らない人
はいないだろう）が振り子時計 Horologium Oscillatorium(1673)にその理論を発表した。
先ほど述べた上の問題に関しても、質点の集まりとして剛体を考えたので
上のような単振り子の集合体を考えるときも、今までの剛体の議論を用いることができるので、
分子はOまわりの慣性モーメント、分母はｈが重心の位置を表すので、それを考慮に入れると
上の式が得られることはわかるだろう。
つまり、上の式からその長さを持った単振り子の運動と同じになることがわかる。
（補足）単振り子
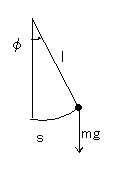
この長さをｓとすると、接線方向の運動方程式は
この長さは
であるので