４．１ 固定点のまわりの回転を考える前に
固定軸の周りに回転する剛体関して、回転を表す角運動量を表現すると
となり、慣性モーメント I を用いることで表現することができた。
ここでの、慣性モーメントとは回転のしやすさを表す量であった。
固定点を持つ剛体に関しても、現実問題、回転のしやすい物体とそうではない物体がある以上、
その回転運動の変化の難易を与える量があるはずである。
今後、それに関して調べていくことにする。
まず、以前にも述べたが剛体の運動をもう少し詳しく考察してみよう。
図のように固定された点Oの周りを自由に運動することができる剛体（灰色のほう）が
あるとして、点Oを中心として、どんな大きさでもいいのだが剛体とともに回る球を設ける。
（内部でなくてもよい）
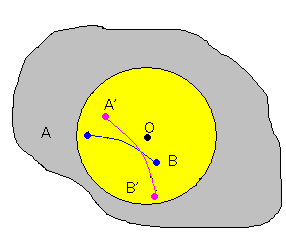
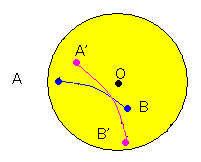
（図1） （図2）
図2に見られるように、剛体の点Aと点Bに着目したとき、大円の弧ABを球状に書くとする。
（大円とは球の断面が最大になる円のこと、つまり原点を通る円）
剛体の運動は結局、この弧の運動を調べれば十分である。
では、この弧の運動を考えてみることにしよう。
この点Oを中心として、微小時間dtだけ回転させたときこの大円の弧ABは弧A'B'に
移る。まずいきなり弧全体の動きを追うとわけがわからなくなるので、
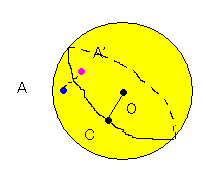（図3）図3のように、点Aのみの動きの変化に関してのみ追うことにしよう。
では、点Aから点A'に中心を通る軸で移動させるとき、軸はどこにあればいいのか？
それは、点Aと点A'を通る大円の弧を垂直に二等分する大円の弧を考えて、その弧上に
ある点Cと点Oを結んだところが軸になる。だから、点Cとなりうる点は無数に存在する
ことになる。
（この弧上以外の点は無理なのかというと無理なんですよね〜〜
ちょっと考えてみるとわかりますが、ヒントは点Aと点A'ともに通る断面の一つを考えて
みよう。断面である円の中心が軸OCの一部になってるんですよね。そこで断面の全体
を連続的に考えるとわかるとは思うんですが・・・）
また、点Bに関しても同様に軸となる点は大円の上に出てくることは理解できるだろう。
図は汚いので当てになりませんが、まぁ大体こんな感じ。
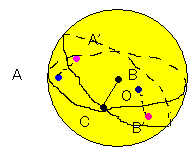
よってこの二つの交点Cと点Oを軸とすれば、点Aから点A'に、点Bから点B'に両方とも
移動させることができる。
以上より、
非常に短い時間内の剛体の回転は一つの軸OCのまわりの小さな回転である。
ということが結論付けられる。
当然大円の交点は2つあるのだが、剛体の回転に対して右ねじ回りになるほうを
とする。
４．２ 角速度と速度の関係
固定点の剛体の運動に関して回転軸が重要であることは理解できただろう。よって、
この回転軸に関してもう少し考察していくことにしよう。そして、その回転軸に関する
新たな角速度ベクトルを定義して、速度との関係を見ていく。
今度はまた下の図を考えてほしい。
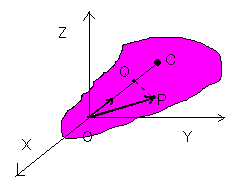
OCの周りの回転角を
とすれば、角速度は
で与えられる。（当然右ねじ周りの回転を考える）
いま、
の方向に大きさ
を考えて、これを角速度ベクトルと名づける。 剛体内の任意の点をPとして、その速度ベクトル
とし、OP＝ｒ、∠POQ＝θとする。PQを半径にして回転するので、
であり、方向は面OPQに垂直であるので、これより、
であることがわかるだろう。
４．３ 角運動量に関する運動方程式
剛体の運動は成分で考えたとき、三つの重心の運動方程式と三つの角運動量の
時間変化の方程式を解析すれば、剛体の運動を解けたことになり、重心の運動方程式
に関してはこれを解くこと自体はそれほど難しくはない（必ずしも解けるとは限らないが）、
しかし、角運動量の時間微分の式はこのままでは全くといっていいほど、
解けそうにはないことは以前述べた。
そこでこの節では、角運動量の式を角速度ベクトルと速度の関係を用いて少し変形
してみることを試みる。
剛体が固定点Oの周りで角速度
で回転しているとき、まず速度ベクトルに関して成分で書いてみると、
角運動量の式に関しては成分で書いてみますと、
であるから、速度に上式を代入しますと、
ただし、
このように変形することができた。
おいおい、これじゃあ、余計、この時間微分の方程式が複雑になって
解けなくなってるんじゃないの？と思うかもしれないが、この式の詳しい考察の前に、
準備しないといけないことが多くある、ということをちょっと了解してもらいたい。
（目的を見失わないでほしい、この角運動量の時間微分の方程式を解くこと
にあるということを・・・・・）
ところで、この角運動量の式をよ〜く見てみると、
角運動量の式は角速度の成分に線型で、係数が対角線に関して、対称になっている。
また、対角成分A、B、Cに関してはｘ、ｙ、ｚ軸の回転に関する、
慣性モーメント(moment of inertia)と呼ばれるものである。
F、G、Hは慣性乗積(product of inertia)と呼ばれている。
この性質がなんか関係してくるのかな、しないのかな〜〜
準備１ 慣性楕円体
