運動量


２．１　はじめに
　　　　物体を扱う上でこの力学では二つに分類して、話を展開する。
　　　　まずはじめに、質点（質量は持つが大きさは持たない、つまり点とみなす仮想的な物体）
　　　　の運動を考える。
　　　　質点の運動がある程度理解できたら、次に剛体（質量と大きさを持つが、力を加えても
　　　　変形しない仮想的な物体）
　　　　の運動に関して述べていくことにする。剛体は質点の集まりとして議論するので、
　　　　まず質点の運動をきちんと理解する必要がある
　　　　以下は、質点の運動に関して書いたものです。

２．２　運動量
　　　　よく日常で使う物理量は、速度、力、距離などがあるが、次の量を定義する。
　　　　　　　　　　　　　　　　　　　　
　　　　を運動量(momentum)といい、運動方程式は
　　　　　　　　　　　　　　　　　　　　
　　　　とかくことができ、質点の持つ運動量の時間変化が働く力に等しいことを言っている。
　　　　は質点に働く力の合力であるが、この合力が0、つまり何も力が働かないときは
　　　　　　　　　　　　　　　　　　　　
　　　　となる。つまり、運動量が保存する。これを、
　　　　運動量の保存則(law of conservation of momentum)
　　　　という。この法則は質点が多いときに重要になる。このことはあとで詳しく述べる。
　　　　

２．３　力積
　　　　次に、運動量に関係した運動方程式において　　から　　まで
　　　　時間に関して積分してみることを考える。
　　　　　　　　　　　　　　　　　　　
　　　　は力積(impulse)と呼ばれ、ベクトル量である。
　　　　この式の言っていることは、運動量の変化量はこの力積を計算することに等しい
　　　　力を加えるとき運動は変化するが、その変化は、質量の大きいものだったり、
　　　　より速度を変化させるときに、より大きい力が必要になるし、時間も当然長くなるということ
　　　　を上の式はいっているわけだ。
　　　　運動の変化というものを、速度だけで捉えていてはいけない。
　　　　それは力を加えた時に運動は変化するが
　　　　それは速度にも、質量にも関係しているわけだから、新しい物理量として、
　　　　その両方を兼ね備えた運動量というものが導入されることはごく自然なことでもある。
　　　　
　　　　ところで、野球のボールをバットで叩くときのように、質点に働く力が短時間で、
　　　　非常に大きな力であるとき、この力を撃力(impulse force)と呼ぶが、
　　　　具体的に時間の変化に対してどのような力が働くのかを知るのは
　　　　、一瞬の時間に力を色々と測定しないといけないので難しい。多くの場合は、
　　　　そのような測定は必要なく、運動量の変化から力積を求めて撃力の効果を理解する。


２．４　運動量保存則
　　　２．４．１　内力と外力
　　　　一つの質点に関する運動量の保存則に関しては、上に述べたように、その質点に力（外力）が
　　　　働いていないならば、運動量は保存することはしった。
　　　　では、二質点あるいは多数の質点があるときには、運動量の保存則はどうなるのだろうか？
　　　　まず、二質点に関して、運動量保存則を考えてみよう。
　　　　その前に、外力と内力の二つの力の違いについて説明することにしよう。
　　　　
　　　　　　内力(internal force)
　　　　　　内力とは、体系内のほかの質点から受ける力のことを言う。
　　　　　　つまり、着目している物体全体を見たとき、それらの物体のそれぞれが作用しあう力がある
　　　　　　（万有引力とか）。そのような力の全体の総称を内力という。
　　　　　　
　　　　　　外力(external force)
　　　　　　外力とは、内力以外の体系外から作用する力の総称のことを言う。
　　　　　　例えば、外部からの電場とか、体系に入っていない物体からの万有引力とか
　　　　　　（万有引力だからといって内力になるわけではない）このような力の総称を外力という。
　　　　
　　　２．４．２　二質点における運動量保存　
　　　　　これから、i番目の物体に働く力の中で、k番目の物体から働く内力をと書き、
　　　　　i番目に働く外力の総和をと書くことにする。
　　　　　1番目の質点の運動方程式は、
　　　　　　　　　　　　　　　　　　　
　　　　　2番目の質点の運動方程式は、
　　　　　　　　　　　　　　　　　　　
　　　　　となっている。この二つの運動方程式の両辺を足し合わせると
　　　　　　　　　　　　　　　　　　　

　　　　　内力に関しては、運動の第三法則（作用反作用の法則から）
　　　　　　　　　　　　　　　　　　　
　　　　　ここで、この計算を用いると上の式は
　　　　　　　　　　　　　　　　　　　
　　　　　つまり、系全体の質点の運動量が時間に対して変わる割合は、
　　　　　これに働く外力の総和に等しく、内力の影響は全く受けことを意味する。
　　　　　また、外力の総和が0になるとき、二つの運動量の和は保存する。
　　　　　もっと多くの質点に関してもこのことは成り立つことは容易に示すことができるので、
　　　　　ここでは割愛する。（上と同じような考え方でできますよ）

　　　２．４．３　多質点における運動量保存　
　　　　　i番目の運動方程式が
　　　　　　　　　　　　　　　　　　　
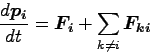
　　　　　この式でというのは、質点が自分自身に力は及ぼさないということ。
　　　　　（万有引力はそのような性質を持つということ）
　　　　　さっきと同様にすべての質点の運動方程式の和を取ると、
　　　　　　　　　　　　　　　　　　　
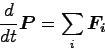
　　　　　　ここで
　　　　　　　　　　　　　　　　　　　
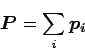
　　　　　というのは全運動量を表す。
　　　　　これらの式をよく見てみると、重要な結果が得られたことになる。それは、
　　　　　今考えている系において、全質点の運動量の時間にたいしてする変化量は、
　　　　　これに働く外力の総和に等しく、わざわざ、内力の影響を考えなくてもよい。この結果は、
　　　　　剛体が斜面を落ちるときの重心運動を調べるのにいちいち内部の効果を
　　　　　考えなくていいということ。逆にそんなことを考えたら大変だ。運良くも調べなくていいのだ。
　　　　　またここでも、外力の総和が0ならば、全運動量が一定に保たれる。
　　　　　このことを、運動量の保存則という。

　　　　　なぜ重心といったのかというと、上の式で、以下のように変形してみる。
　　　　　　　　　　　　　　　　　　
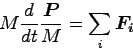
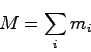　　　　　　　　　　　　　　　　　　　　は全質量
　　　　　　　　　　　　　　　　　　　は重心の速さ
　　　　　であるので、重心の速さを表現しているからだ。つまり、重心の運動方程式そのものを
　　　　　表していることに気づくだろう。だから、重心の運動といったのだ。
　　　　　これを見ると、
　　　　　質点系（多数の質点の集まった系）の重心の運動は重心に全質量が集まり
　　　　　、外力がその一点のみに作用する単なる一質点の運動に等しい。
　　　　　という単純なモデルに置き換えることができる、という点で重心の運動を考えるには
　　　　　意味がある。
　　　　　重心に関してはまた、補足のところに考察してみるのでそこを参考にしてほしい。