3.1 はじめに
この節は、Newton方程式の解き方について学ぼう。
高校までは、一次元の運動しか扱わなかったり、イメージしやすい運動しか扱わなかったので
たいして、運動方程式を解いた後、符号が違っても無視したり、それを解くことに苦労しなかった
人も多いかもしれない。しかし、実際これから運動がイメージしづらいことも現象を扱うことも多く
なっていくと思うので、ここできちんと解き方を理解してもらいたい。特に符号の間違えは命取りだ。
3.2 運動を知ること
運動を知りたいと思ったとき、(運動を知るということは、ある時間にどこにいるかを知ることだ。
もっとも、数学的に言うと位置を時間の関数で表すこと)
まずある運動に影響するのは何かを考えると、
当然、運動はある時間に力がどのようにかかっているかによって
どの程度加速されるかが決まる。
この関係は運動方程式によって与えられることは知っているだろう。
しかし、これだけでは運動が決まるとはいえない。それは最初の条件によって
運動は異なる軌道を描くからだ。大雑把に言うと(抵抗を考えなければ)ボールを投げるとき、
ある時間にかかる力は一定ではあるが、初速度、初期位置、が違えばどこまで飛ぶかは異なる。
(そりゃ当たり前だ)
つまり、運動を決めるには運動方程式(微分方程式)を解くことと、二つの初期条件が必要
ということになる。
次に問題であるのが、自分で運動方程式を立てるということが重要になってくる。
これさえできれば、後は機械的に運動方程式を解くだけ。(すべてが解けるとは限らないが)
この式を立てる上で問題になるのが何かを、想像してほしい。
この式で重要なことは力から加速度を知ることにある、その逆ではない。
当たり前のことだが、加速度が分かれば運動は決定されてしまうものだから
基本的な流れは力がわかってて、そこから加速度を得て、初期条件を考慮して運動が決まる。
簡単に書いてあるが問題なのが、一番最初に書いた、力がわかるということだ。力を理解するには
どんな力がどのようなときにどう作用するのか?ということを理解しなくてはならず、またすべての
力を考慮に入れないとマッタク違った運動を見せることになる。
つまり、運動を知るということは作用している力を理解することがすべてだといっても過言ではない
3.3 単振動
図のようにばねの一端が原点が固定されていて、もう一方に質量mの物体がついているとする。
ばねの自然長の長さをl、ばね定数をkとする。
ばねは自然長からの距離に比例する力を及ぼす。物体に働く力は、
物体が位置xのところにいるとき、
従って、
となり、運動方程式は
となる。このように、運動方程式を立てるときは、力の方向と、その力の性質(今回はばねの性質)
に注意しないといけない。
次は、運動方程式を解くことだが、ここからは数学だ。
運動方程式は
となり、この微分方程式の解は、
であるので、
として解ける。
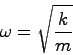 としている。
としている。Aと
未知定数が2つあり、条件式が2つあるので、決定できるのはわかるだろう。
例えば、初速度がなく、初期位置が2lにいるような場合。初期条件は
以上より、
として、決定される。これは
