角運動量
５．１ ベクトルの外積
二つのベクトルの外積とは、二つのベクトルが作る平行四辺形の面積に等しく、かつ、二つの
ベクトルに垂直な右ねじ方向のベクトルのこと。
このような要請から教科書に出てくるよくあるあの複雑な式が得られる。ここでは、これに関しては
解説しない（そのうちするかも）
５．２ モーメントと回転
今まで、てこの原理というものを理解してきたことがあるだろうか？
小、中、ましてや高校のときでも、支点から作用点までを結んだ直線の距離とその直線に垂直に
作用している力の成分を掛け算したものが回転を表す量だと覚えこまされる。
人間とは面白いもので、実際きちんと考えもしないくせに、試験や学校で正しいといわれ、答えが
あっていたら、本当に正しいとよく思ってしまうものである。
今日はせっかく読んでくれているのだから、そんなに難しくないのできちんとこの量について考え
て見ることにしよう。
モーメント（moment）という量を次のように定義する。
この定義は、上の文章で書いたこととおなじことである。
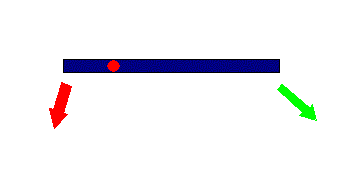
図に書いてある二つの力を考えると、このうちこの支点を中心に回転させる効果は明らかに力の成
分のうち棒に垂直な成分のみが効果を持つことはわかるだろう。それは、釣り合っているときに
この棒に平行な力をいくら加えても棒が回転することはない（釣り合いを保ち続ける）。
次に問題となるのが、なぜ、力と支点からの位置ベクトルの外積になるのかということを、考え
てみる必要がある。そこで、次の図を見てもらいたい。
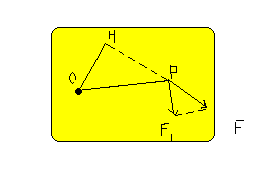
この四角で囲まれた物体を、Pに力を作用させて回転させるとき、今までの議論から
回転に関係するのは、
でも、
でもどちらを考えても回転させる能力は一緒であるはずだから、二つの直角三角形の相似の条件より、OH=a , OP=b
ということになり、これは、回転させる効果を表す量が
支点と力の作用線までの距離と、力の大きさを掛けたものであることを暗に意味している。
（作用線とは力の方向上にある直線のこと、つまり
なら、直線PHのこと）以上のことを数学的に記述すると、外積を用いなくてはならず、それは
と書き、これを力のモーメントと呼ぶ。
５．３ 角運動量
力のモーメントが力がどの程度回転に影響を与えるかを表す量であった。
今回学ぶ角運動量とは誤解を恐れずに言うと回転の勢いを表現する量である。
この量は、剛体の運動を表現するときに欠かせなくなる。
（想像してほしいのだが、剛体の位置を表現する
ことを考えたときには、つまり運動を知るには、いかなる剛体も、剛体の重心の位置とその
剛体がどの程度回転しているのかを表す二つの設定が必要である。
すなわち、あるひとつの剛体が違う位置に移るとき、平行移動と回転移動
で表現できるということ）
というわけで、回転に関係するこれらの量は十分に学習したいところだ。
（後で上に書いてある意味が剛体を勉強するときに理解できると思う。）
では本題に入ることにしよう。
角運動量（angular momentum） L という物理量を今から以下のように定義する。
角運動量とは、位置ベクトルと運動量の外積とする。
ここで、モーメントの
のところに 
を代入している。当然これを読んでいる人の中には、疑い深い人もいるとおもう。その人はこんな量が本当に
回転の勢いを表す量なのかと？
これに答えるのは難しい。
でも、よく考えてほしいのが、物体を回転させるとき、同じ速さでも腕の長さが長いほど、
または、質量が大きければ大きいほど回転させるのは余計に労力が必要であることと、
速度に関してでも、速度は腕に関して垂直成分しか回転に影響しないことを考えると
上の定義の仕方は正しいそうだ。
また、回転を表す量なら力のモーメントと何か関係があってもよさそうだ。L を時間微分して
みると、
速度ベクトルと運動量ベクトルが平行なのと運動量の時間微分が力なので、
となり、右辺は力のモーメントになっている。
このように時間微分すると力のモーメントになる量のことを角運動量という。
また、こうもいえる
原点Oまわりの角運動量が時間とともに変化する割合は、この質点に働いている力の
Oまわりのモーメントに等しい。
また、
質点に働く力のモーメントが０であるなら角運動量は一定値を取る。
これを角運動量保存則という。
一見、あまり答えになっていないような気がするが、そもそもこのような導入の仕方は
運動量の導入の仕方とよく似ている。運動方程式から
として運動量を定義した。
じゃ運動量は何かというと、運動の勢いというしかなく、日常それほど使わない量
（速度とかと比べて必要でない量）なので直感的にしっくりと理解することはなかなか難しい。
慣れてくればこの量というものがごく自然なものになっていくのじゃないだろうか。
ただいえることは、運動量も角運動量も物理現象を記述してくには、今後重要になる物理量
なので、ここできちんと定義しておいた。
とりあえず、角運動量というのは、回転の勢いを表す量で、運動量は運動の勢いと考えることが
一番望ましいと思う、以後また理解しやすい考え方があったら述べることにしよう。
５．４ 角運動量保存の法則
一質点に関しての角運動量に関しては、力のモーメントが0ならば保存することは見てきた。
ではより一般的に、多数の質点を考えたとき、（剛体の運動に必要になってくるため）
角運動量の保存則はどうなっているのだろうか。運動量保存則と同じように、内力に関しては
考える必要があるのか？また、重心との関係はどうなっているのか？という疑問が出てくる。
内力に関する力のモーメントも考慮しないと、角運動量に関して記述できないとすると、
これは、剛体の運動を調べるときに内力まで考えなければいけなくなり、運動を解析する
ことは複雑になり不可能だ。だが、日常よくある運動を考えるとき（ボールを投げるとか）
誰も内力の効果に関して口にする人はいない、例えば、変化球を投げるときでも抵抗は
考えても（外力）、内力の効果について口にするのは誰もいないだろう。
それだけで、内力を考えなくていいと結論づけるわけにはいかない、なぜなら、内力の効果が
小さいがあるかもしれないからだ。よってこれからこのことについて考えてみることにしよう。
５．４．１ 角運動量の保存則
いま、原点まわりの角運動量を考えて、すべての質点において
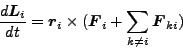
が成り立つことは、一質点のときと同じである。i番目の質点に働く外力を
としk番目の質点からi番目に作用する内力を
と書くことにしている。ここで、すべての質点に関して和をとると、
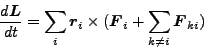
としている。運動量を考えたときのように、一見、内力の効果を消すことができないように見えるのだが、
内力の力のうちで、
に着目して、この和の中には以下の項が一対ずつある。
自分で i が３ or 4ぐらいのときを試してみるとよくわかるだろう。
あることを確認したら、Newtonの第三法則、（作用反作用の法則）を思い出してみると、
＝ 
であるが、この位置ベクトルと力のベクトルは実は第三法則によって平行になっている。
位置ベクトルは、i番目からk番目に向かうベクトル。力もその方向に向いている。よって、
ということは、内力の効果はすべて打ち消されて、
となる。
結論は、
質点系における、角運動量が時間とともに変わる割合は、この質点系に働いている
外力のモーメントの和に等しく、内力は無関係である。
しかも、外力のモーメントの和が0になるときは角運動量は保存される。
以上の結論より、やはり内力の効果に関しては気にしなくてもよかったわけである。
ここで、角運動量が保存していると便利なことがある、それは何かというと、一般には
三次元の運動として扱わなければいけない質点系に関しても、二次元の平面運動として
扱うことが可能になるという点である。
これはどういうことかというと、運動方程式をｘ、ｙ、ｚに関してどれか一つ解かなくても
よいということになる。おおっ、なんて便利なんだ。
例えば、太陽と地球の運動に関して、他の天体からの作用は惑星間の距離が大きいので
ほとんど受けていないと考えることができる。（細かく考えるときは考える必要があるが）
ゆえに、外力が働いていないと考えても差し支えがなく、平面運動をすると
考えてもよい。（角運動量が保存しているので）
この理由に関しては（ここで議論することではないので）
補足の中心力と面積の原理で述べよう。
５．４．２ 角運動量と重心の関係
重心の運動は比較的簡単に求められることを、運動量の節で述べた。
つまり、重心にすべての質量が集まったと考えて質点の運動と考えることで求めることができた。
だから、物体の運動を考えるとき、重心の運動と重心まわりの運動とに分けて考えることが多い。
角運動量に関しても同様に重心に関してはどうなっているのかを考えてみてみよう。
原点周りにとった質点系の運動量Lは
によって与えられる。質点系の重心の位置を
とし、重心からのi番目の質点までの位置ベクトルを
とする。
速度ベクトルに関しては
全質量を
と書くことにすると、角運動量のところに代入すると、
もし重心を原点に持ってくると、重心の公式を思い出してみると、
であるので、その分子である量は0になる。
では、重心
と重心からの距離 に分けたあとでも は重心を原点と見たときの距離であるので、
は０となり、この微分である 
も0になる。この考え方は以後よく使うのできちんと理解してもらいたい。
ゆえに、第三項と第四項はおちる。
ここで、
は重心まわりの角運動量、
を意味している。プライム（’）は重心からの距離を意味しているから。
角運動量の時間微分を考えてみる。
第一項に関しては同じベクトルの外積なので、0になる。
ところで、モーメントに関しては
であるので、ｄL/dt＝Nなので、
が導くことができる。
この結果は重心のまわりの角運動量の時間変化は重心を基準とした外力の
力のモーメントに等しい。
しかし、この結果は、やる前から実はわかっていたことでもある。（なんですって！！）
以前導いた、原点を基準にした角運動量と力のモーメントの関係を思い出してほしい。
あのとき、どの点に関して注目しただろうか?それは本当に原点のみなのだろうか。
いやそうではない。それは人間が勝手に決めた主観的な基準点であり、
ある状態を持ってきたときに、ここが原点ですというような
特別な点は存在しない、いままで、特に疑問に思わなかった人もいるだろうが、
座標を設定するときに、原点をここにしないといけないといわれたことがあるだろうか?
それはないはずである。つまり何が言いたいかというと、基準とする点とはテキトーに
とることができるのである。今回は重心という特別な点を基準としてみたら、重心を基準とした
同じ式が出てきて当然なのである。ということを最後に付け加えておこう。
