1.1 剛体の運動を解くにあたって
剛体の運動を解くということは、剛体の任意の点が時間変化に対してどのように変化していく
のかを知る必要がある。これを知るためには、剛体の任意の点をまず表現する必要がある。
例えば質点だった場合は、この点を表現したいならば三つの座標を設定すればよかった。
そして、三つの運動方程式(x、y、zに関して)を解くことによって、運動が決定したのだった。
では、剛体だった場合はどのように任意の点を表現すればいいのか?
実は表現の仕方はいくらでもあるのだが、その独立な座標の数は決まっている。
それは六つである。
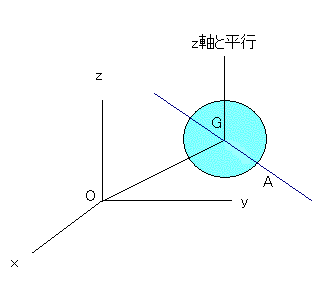
上の剛体を見てほしい、剛体の位置を表現することを考える。
まず、剛体の基準となる重心G(重心でなくてもいいのだが)を決める必要がある。
これにより、三つの座標が必要となる。そして、最初に剛体の重心を通る任意の直線GA
を決めて(串刺しにしておいて)、この直線を決めるために、この串刺しにされた直線とz軸の
なす角を決めるためと、方位角(z軸を含む面のz軸まわりの角)の二つを決める必要があり、
最後に直線GA周りの回転を決めるのに六つ目の変数を用いる。
以上の考察より、
剛体の運動を調べるには6個の自由度(表現するための座標)があればよい。
ということが結論付けられるだろう。
このことから次のことが言える、ある位置を指定するのに6個の自由度があるなら、これを時間の
変化に対してどう動くのかを調べることが運動を解くことなのだから、六個の自由度を時間に対して
指定することが必要である。結局
剛体の運動を調べるには六個の独立な方程式を解くこと
が必要になる。
では、六個の運動方程式とは何であろうか?
それはまず、重心の運動方程式である。(重心の座標を指定するため)
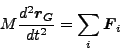
角運動量の式
これらの式が、六個の方程式の役割を果たす。(成分で分解してみよ)
これに関しては、少し疑問を持ってほしいことがあるのだが、それは何かというと、
上の重心の運動方程式に関しては、力が複雑でないならば一成分ごとに考えてあげれば
簡単に解くことはできるだろう。
しかし、角運動量の式に関しては全角運動量を表すLは成分を思い出してほしいのだが、
変数の数が異常に多い(教科書で確認してみよう)、しかも力のモーメントの成分に関しては
座標まで入っている。(微分方程式を少し勉強したことがある人にとってはこんな形の微分
方程式を解くことは不可能であることは、本能的に察知することはできるだろう)
結局この運動方程式のうち変数を減らすこと(簡単にまとめることが)唯一の解決策
なのである。
そのために、慣性モーメントという量を定義して簡略化することが図られるわけである。
慣性モーメントに関しての詳しいことは後に述べよう。
1.2 剛体のつりあい
剛体のつりあいを考えてみることにしよう。釣り合いとは何かというと、時間に対して運動が
変化しないということだ。つりあっていれば、未来永劫、同じ運動を保ち続けるということだ。
注意しておくが、物体が止まっているということではない。これはつりあいの状態のうちの
一つの状態だ。
では、つりあうためにはどのような条件が成り立っていればいいのか?
質点に関してまず考えてみると、運動が一定になるには、加速度が一定であればよい。
よって、
この時、
が成り立つ。つまり、質点に働くすべての力の合力が0になるような場合はつりあっている
という。
では剛体に関しては、どうなっているのだろうか?
まず、重心の運動が加速していればこれは明らかに未来永劫運動が変わらないとはいえない
だろう。よって、
は質点と同様である。
でもこれだけでは十分ではない。回転に影響を及ぼすような効果はあってはならない。ゆえに、
である。以上の結果より、剛体のつりあい関しては以下の式が成り立つ。
ということは、剛体がつりあうには、働くすべての力の合力が0、かつ力のモーメントが0に
なる必要がある。
しかしこの条件だけで十分なのか?と疑問を持つ人もいるかもしれない。
だが思い出してほしい、剛体の運動を記述するのは六つの方程式があれば十分だったことを、
上の条件式は明らかに六つの条件が入っているので、これで十分なのである。
