2．１ 固定軸を持つ剛体の運動
剛体がある直線周りに回転運動するような場合を考える。図を見ていただきたい。
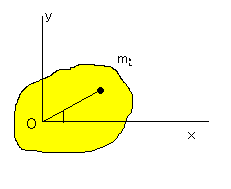
この図は、剛体を ｚ軸方向から見ています。
今回、ｚ軸回転しか考えないので、z軸周りにどの程度回ったかで剛体の位置は決まる。
つまり、自由度が一つである、ゆえにこの自由度を決めるのに運動方程式が
１つ必要となる。
この運動方程式はz軸の回転なわけだから、z軸の角運動量の式を使えばいい。
z軸回転なので円柱座標を用いて、
、 
これを時間に対して微分すると、距離は時間に対して変化しないことに注意すれば、
、
しかも、
はある点に関する角速度であるが、どの質点に着目しても、その角速度は剛体であり、軸が固定されていればそれは一定になる。その角速度を
とすると、
、 
よって、z軸の角運動量に関しては、
であるので、これらを代入すると、
となる。そこで次の量を定義する。
剛体の力学では重要でよく出てくる量であり、この量を、
慣性モーメント（moment of inertia）という。 今回この量の意味することは
次の式を見てみると理解できると思う。
慣性モーメントを使うと
と書ける。これから、もとのz軸の角運動量の式に代入すると、
または、
と書くことができる。
この式をよく見てみると、加速度の時間変化（回転のしやすさ）は力のモーメントの
大きさに比例している。また、慣性モーメントの大きさに反比例することがわかる。
このことから、慣性モーメントの大小で、その物体の回転のしやすさが判断できる。
慣性モーメントの定義式を見てみればわかることだが、同じ質量があったとしても、
その質量が軸から遠くに離れていれば、慣性モーメントが大きくなり物体は回転しづらい
物体であることは、容易に理解することができるだろう。
以上より、慣性モーメントとは剛体が回転しやすいかどうかを判断するための一つの
指標となる量である。
しかも、方程式の形を見てほしいのだが角運動量の形と比べて慣性モーメントが計算
できれば、よりスマートな（解きやすい）方程式の形になっているというメリットも
理解できるだろう。
最後に、今回上の式で、力のモーメントの成分を書くことはしなかったが、
（つまり、添え字をつけることをしなかった）
注意したいのは、この力のモーメントの成分は回転している軸方向の成分しか
取らないということである。
2．2 エネルギー保存則と仕事
運動を考えたとき、やはり、エネルギー保存則や仕事を考えないわけにはいかないだろう。
というわけで、この節はそのことについて少し議論してみることにしよう。
固定軸周りに関しての角速度を
とすれば、
の速さは
となるので、この点における運動エネルギーは
でかける。ゆえに、剛体の運動エネルギーは
とかけることは全体の和をとり、慣性モーメントの定義を思い出してくれれば理解できる。
では、位置エネルギーに関しては今回簡単のために保存力が働いているとして、Uと
書くことにしておくと、力学的エネルギーの保存則より、
正直言うと、Uの形はどうなるんだという疑問も在ると思うが、これに関しては、少し考えれば
わかると思うが、きれいな形に表現することはできなさそうである。
というのは、剛体内の個々の点の高さに関して表現するわけなのだが、
それは例えば、個々の点に関して、それぞれ角度を指定してあげ、高さを表現して個々の
位置エネルギーを表現することはでは可能であるが、そこからうまくまとめることが
できないからだ、だからあえて表現しなかった。
まぁ、正直どうでもいいことであるが、運動エネルギーの形は知っておこう。
では、次に仕事に関してはどうなっているのだろうか？
点
で力が成分
が働いているとする。剛体が微小角度回転したときを考える。どの点に関しても
という関係は、剛体かつ軸回りで回転していれば、常に成り立っているわけで、
とおくと、
この力が、行った仕事は
この右辺の形は力のモーメントの形になっていることから、
全体のこの微小回転の間に力がした仕事は
である。
