3.1 慣性モーメントを求める前に
慣性モーメントは物体の回転のしやすさを表すひとつの指標であること。
剛体は六つの方程式(三つの運動方程式と三つの角運動量の式)を解くことによって、運動を決定
することはできるのであったのだが、このうち角運動量のほうが変数の数が多く直接解くことは、
かなり困難だということ、それで慣性モーメントを用いるとある程度簡単な形に帰着できる。
という二つのメリットがあったわけだ。
こんなメリットがあるなら、慣性モーメントを計算できないわけにはいかない。
では、どうのようにこれらを計算すればよいのかという問題が生じる。
軸周りの慣性モーメントは
を計算しないといけない。実際、和の項が多いときの計算というのは、
そのままでは全くといっていいほど計算することは不可能である。
しかし、我々は普通剛体の運動を考えるときは、連続的な質量分布をもった物体を考えることが
多く、そのとき密度をρとすれば、
と、積分の形に書き換えることができる。第二式から第三式の変形は
から理解することはできるだろう。
ほほう、こうしてあげると、結局はρが簡単なら計算することは簡単だ、(実際密度は一定と考える
から、計算はとっても簡単)
これで説明を終わりにしてもいいわけだが、慣性モーメントを求めるとき便利な公式が二つほど
あるので、これに関して少し説明しておこう。
3.2 便利な公式
(1)重心と慣性モーメント
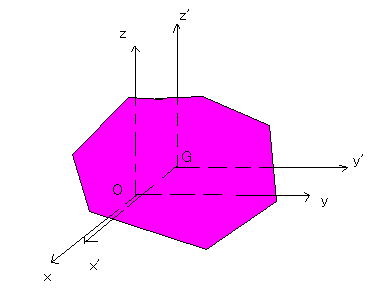
今、一つの剛体のz軸の回りの慣性モーメントを求まることを考える。
慣性モーメントの定義より、
である。このまま求めてもいいわけだが、重心Gを通るz’軸周りの慣性モーメントと
比べてみることにしよう。
であるので、これを上の式代入すると、
重心のところで何度も出てきたように、
であることは、周知の通りである。ということは、第二項はz’軸(重心を通る)のまわりの
慣性モーメントであるため、重心までの距離を
とすると、慣性モーメントは
重心まわりの慣性モーメントと、重心の距離の二乗とその全質量の積の和でかける。
この形を知っておくと便利なのは、重心の慣性モーメントを求めておけば、
平行な他の軸における慣性モーメントは上の公式を使えば一発で出せる。
また、重心まわりの慣性モーメントは対称性を持つことが多く、積分計算するのが
より簡単になることが多いという二つのメリットがあるわけで、この公式はとても
便利なわけである。
(2)平面板におけるx軸とy軸の慣性モーメントとz軸の慣性モーメント
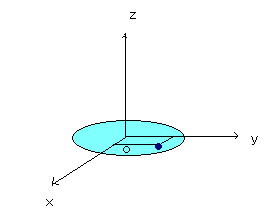
上の薄い板のように、板の面上に原点Oをとり、平面をxy面上に置く、この面に垂直に
z軸がとれる。
であるため、ここからすぐに
であることはわかるだろう。この公式の便利さは次の簡単な例でわかるだろう。
3.3 簡単な例
