剛体の平面運動

　　　　　　　　剛体の平面運動

３．１　剛体の平面運動

　　　　剛体の平面運動とは何かということであるが、
　　　　剛体の各点がそれぞれ、ある一つの平面上に常にのりながら
　　　運動しているということである。
　　　　（円柱が坂道を転がるとき、坂の横から見ると回転しているが、坂の上から見ると
　　　　　回転してはいないような普通の滑り方）

　　　　剛体の位置はどのように決まるかというと、例えば、図のように
　　　　重心の位置と、剛体がこの定平面に対してどの程度回転をしているのかという、三つの
　　　　変数で表現することができるはずである。
　　　　　　　　　

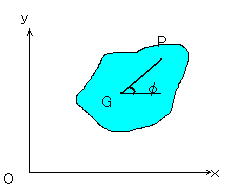
　　　　つまり、変数としては重心の変数二つとこの角度を表すために一つ必要だということ
　　　　がわかる。この変数の決定には三つの方程式が必要で、
　　　　重心の位置は二つの重心の運動方程式
　　　　　　　　　　　

　　　　重心まわりの回転に関しては、z軸周りの角運動量に関しての方程式
　　　　　　　　　　　

　　　　を用いればよい。
　　　　重心の運動方程式の解き方はただ微分方程式を解けばいいだけだから、問題ないだろう。
　　　　重心まわりの角運動量の解き方は、固定軸周りの剛体の運動の場合と同じであるから、
　　　　　　　　　　　

　　　　であるから、上の式は
　　　　　　　　　　　

　または、

　　　　で表現することができる。
　　　　これらの三つの方程式が解ければ、運動は解析できたことになる。

３．２　平面運動でのエネルギー

　　　　重心の運動とその回りの運動と分けて考えるのは、とても便利である。
　　　　今回もそれと同じように考えて、
　　　　　　　　　　　　　　　　

　　　　これを、全運動エネルギーの項に代入してあげると、
　　　　　　　　　　　　　　　　

　　　　となる。以前も何度もやってきたように第二項は重心の性質より、０になることは
　　　　理解できるだろう。（角運動量の５．４参照）
　　　　ゆえに、上式は
　　　　　　　　　　　　　　　　

　　　　ここで、ωは重心から見たときの角速度であり、
　　　　位置エネルギーUの保存力を受けて運動するときには、力学エネルギーの保存則
　　　　　　　　　　　　　　　　

　　　　が得られる。
　　　　この形を使えば問題が簡単に解ける場合もあるが、基本的には３．１節の三式から
　　　　解くことが普通である。エネルギーという観点から解きたいときはこの式を使うとよい。
　　　　しかし、必ずしも万能な式であるわけではない。
　　　　（そりゃ、式が一つしかないわけだから当たり前ではある。）
　　　　

３．３　撃力が働く場合　　　　
　　　　
　　　　質点に関して撃力が働く場合の説明はしたが、平面運動する剛体に撃力が働く場合
　　　　について少し考察してみよう。
　　　　剛体に働く撃力を