丂慜愡傑偱偼丄寢崌攇摦曽掱幃偵娭偟偰媍榑偟偰丄寢徎拞偵俁偮偺岝偑崿崌偟偰偄傞偲偒偵惉棫偡傞曽掱幃偵娭偟偰媍榑偟偰偒偨丅
偱偼偙偺俁偮偺岝偵娭偟偰丄擖幩岝偲偟偰俀偮偺妏廃攇悢冎偑摍偟偄岝傪峫偊丄偝傜偵丄偦偙偐傜俀冎偑弌幩岝偲偟偰惗惉偝傟偨
応崌偳偺傛偆側曽掱幃偵側傞偺偐傪偙偙偱偼媍榑偟傛偆丅
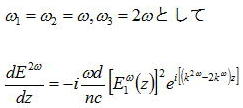
偙偺曽掱幃偼妏廃攇悢冎偐傜俀攞偺妏廃攇悢俀冎偺岝傪敪惗偝偣傞戞俀師崅挷攇敪惗乮SHG:Second-Harmonic Generation)
傪昞偡丅寢徎偲偟偰偼丄KDP寢徎丄Ge傗P傪僪乕僾偟偨偟偨愇塸僼傽僀僶側偳偵傛傞SHG傪婲偙偡丅
忋幃偺曽掱幃傪夝偔偨傔丄娙扨偺偨傔丄倸偵懳偟偰僷儚乕懝幐偑側偔E冎偑堦掕偱偁傞偲偒丄
椺偊偽弌椡抂傑偱偺嫍棧乮寢徎挿乯傪L偲偟偨偲偒丄戞俀師崅挷攇偺揹応偼
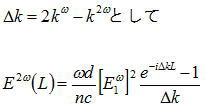
偲偁傜傢偝傟丄弌椡嫮搙偼丄
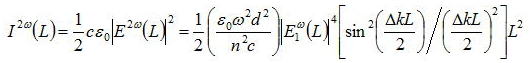
偲側傞丅
壓偺恾偼戞俀師崅挷攇偺敪惗偑嚈倠偵埶懚偟偰偄傞偺傪尒偨傕偺偱偁傞丅
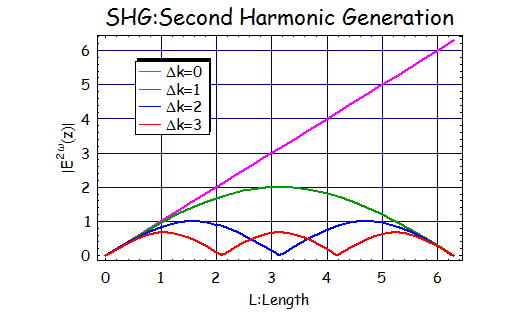
嚈倠亖侽偺偲偒丄戞俀崅挷攇偼寢徎嫍棧傪挿偔偟偰偄偗偽忢偵憹暆偝傟偰偄傞孹岦偑尒偰庢傟傞丅
懠偺嚈倠偺忦審偺偲偒偼丄戞俀崅挷攇偼寢徎偺嫍棧偵埶懚偟偰偍傝丄嵟戝抣偑偁傝丄偦傟埲忋憹暆偡傞偙偲偑偱偒側偄丅
傛偭偰丄埲壓偺忦審傪枮偨偡応崌
寢徎挿傪挿偔偟偰偍偔傎偳戞俀崅挷攇偼憹壛偟偰偄偔桞堦偺忦審偱埵憡惍崌忦審偲偄偆丅
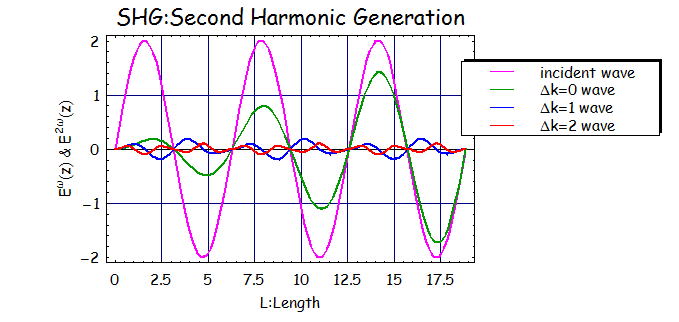
忋偺恾偼擖幩岝傪偄傟偰寢徎傪揱斃偝偣偨偲偒偵寢徎偺挿偝偲偦偺帪偺揹応偺嫮偝傪寁嶼偟偨傕偺偱偁傞丅
擖幩攇偱偁傞incident wave 偼寢徎揱斃偱媧廂偑側偄偲偟偰揹応尭悐偡傞偙偲側偔揱斃偟偰偄傞偲壖掕偟偰偍傝丄
偦偺偲偒丄傗偼傝嚈倠亖侽偺埵憡惍崌傪偲偭偨偮傑傝擖幩攇柺埵憡偲摨偠埵憡偲偟偰揱斃偡傞崅挷攇偺傒偑
憹暆偝傟嫮搙偺嫮偄戞俀崅挷攇傪惗惉偟偆傞偙偲傪帵偟偰偄傞偺偑傛偔傢偐傞乮偲巚偆乯丅
