---

ここでは、光の二重性を見ていくために電磁場を量子化していく。

まずは、調和振動子の量子化にならって量子化を行う。電磁場は、光子の生成・消滅演算子と光子数状態によって記述され

量子特有の期待値や揺らぎの概念を導入して様々な現象を議論していこうと思う。

マクスウェル方程式から得られる平面電磁波は、



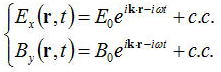
と表され、ｋ＝（０,０,ｋｚ）とz方向に向かう波数ベクトルである。



電場と磁束密度の関係は上式の関係があり、ある体積Vの中での電磁場のエネルギーを考える。

その時に次の電場および磁束密度の次元を表す係数と振幅の大きさを表す無次元の複素振幅ａに分けて、

電磁場の式を以下のように書き換えると、



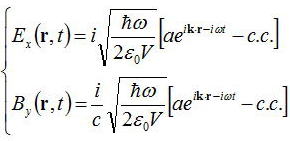
と表すことができる。この式を用いて体積Ｖの直方体の中のエネルギーはｒの体積積分により、



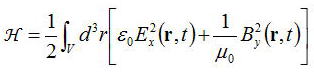
と表される。このようにして、変形した電場と磁束密度の式を代入して整理すると、



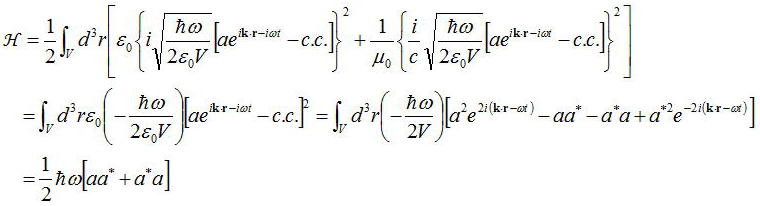
となる。ａ^２とａ*＾２の項が消えているのはｚ方向に対して電磁場の周期境界条件を考えたことによる。

つまり、ｋｚ＝２πｎ/Ｌｚという波を考えている。

こうしてみてみると、エネルギーの形式が量子力学を学んだ方なら覚えていると思うが調和振動子のエネルギー表式と

似ていることが分かる。さらに、そもそも電磁場は正弦波振動であるので力学的な振動を表す

調和振動子と似た形式をとることは想像に難しくないだろう。そこで、電磁場を量子化するにあたって

調和振動子を量子化したときと同じ手続きで行ってみようと思う。

運動量と位置座標は古典論では互いに単なる値なので交換可能であるが、

量子力学では、運動量が微分演算子なので運動量演算子と位置座標演算子は交換可能ではない。

以下であらわされる交換関係というものがある。



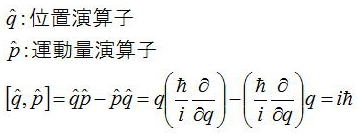
a、a†はp、qを用いて以下のように定義される。



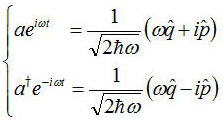
ｐとｑの交換関係をaとa†を用いて書きなおすと



となり、この交換関係を満たすaとa†を用いて電磁場を量子化して、総エネルギーを表現しなおすと



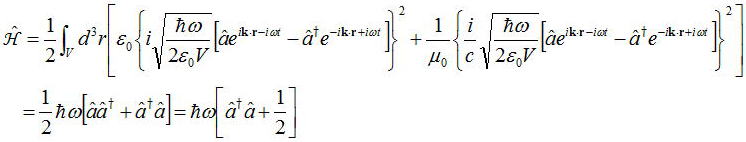
とすることができる