---

吸収飽和：密度行列方程式における定常解

前節では、遷移による分布がすべて基底準位（Ground State）にあるとして電気感受率χを計算してきた。

しかしながら、実際は光が入った際にすべてが基底準位にあるということはない。そのため、各準位における分布がどのように

感受率に影響を与えるのかを知っておく必要があるだろう。

各準位における分布の影響は密度行列の対角項である。



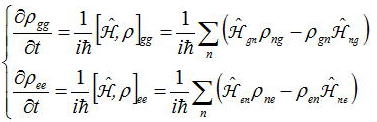
非対角項で扱った緩和の影響と同様に、励起準位ｅにある分布が基底準位ｇに落ちてくる効果を表す必要がある。

この影響を緩和定数Γとする。この効果を取り入れて、前節同様に回転波近似と電場の項と非対角項をフーリエ分解しておいて



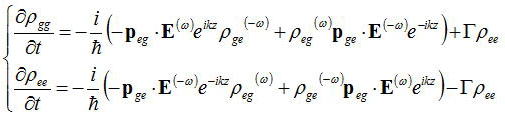
となる。これらの差をとると



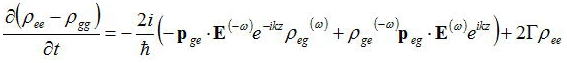
また、この式と前節導いた以下の式、



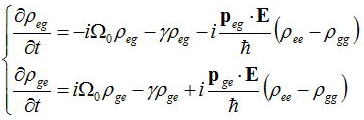
を用いて、定常状態になったとして、時間変動項を０として扱い上式の連立方程式を解くと



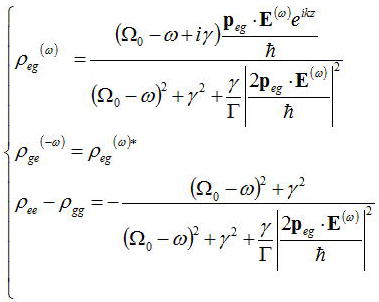
を得る。非対角成分の求めたので、ここから巨視的双極子モーメントをこれも前節と同様に計算すると



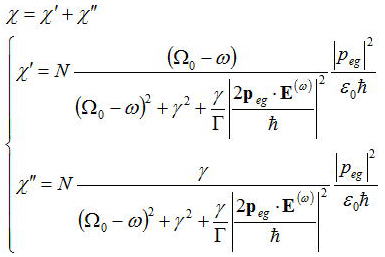
となる。上式のχ”に着目すると電場の二乗の効果により、電場が強くなるとχ”の値が小さくなることを意味する。

つまり、電場が強くなることでＥの方向へ分極が向き、最終的にはその分極が飽和していくことで

それ以上光を吸収して分極をＥ方向へ向かせることができなくなり、光吸収が飽和することを意味する。

さらにポピュレーションの差をみると電場が大きくなると、ρｅｅ−ρｇｇ＝０となり、ρｅｅ＋ρｇｇ＝１から、ρｅｅ＝ρｇｇ＝１/２

となる。これの意味するところは、ある原子に光をどんなに強く入射しても励起準位が基底準位の分布を上回ることがないこと

を意味している。

　では、今後レーザの節で述べるがレーザが発振するには反転分布、つまりρｅｅ＞ρｇｇにすることで、吸収から

光放出する媒質状態に変えてあげることでレーザ発振が行われる。この条件を満たすためにはどのようなからくりがあるのであろうか？

これに関しての詳細は次節に述べるが結論だけ言うと、

今は２準位系を考えているが、２準位系ではレーザは発振しなく、３準位系や４準位系と呼ばれる系を考えることでさらに上の準位からの

ポピュレーションの緩和により電子が中間準位にもたまることになり、反転分布を形成することが可能となる。

　さて、上式の電場の２乗の項に関して展開していくとχが電場の二乗の多項式で展開できることになる。つまり、

χ＝χ0＋χ2＊Ｅ＾２＋χ４＊Ｅ＾４＋・・・・・・

となる。これは、非線形効果と呼び、吸収や分極の飽和は非線形効果のひとつであると考える。

最後に上式のχの様子を弱電場と吸収がある場合とで比較した図を下に示す。



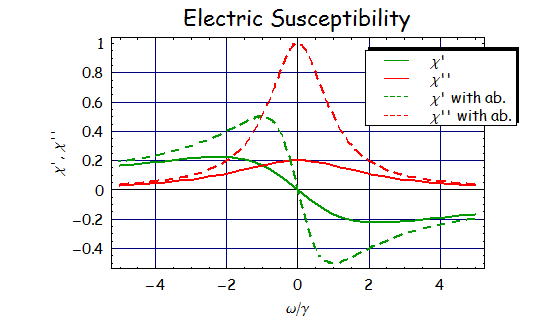
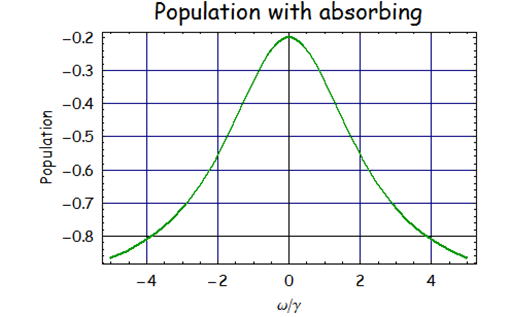
上記に示すように、感受率において吸収がある場合とない場合の比較をしてある。

吸収量と直接関係のあるχ’’は減少し、吸収が飽和しているのがわかる。さらに屈折率に直接関係するχ’の共鳴周波数近傍での

屈折率変化の割合が鈍くなることが分かる。右図は左図の変化を見せるときのポピュレーションの差分量（ρｅｅ−ρｇｇ）である。