
傑偢偼偠傔偵
丂偙偺愡偱偼崱傑偱俀弨埵宯偱偺媧廂偲偦偺媧廂帪偺揹婥姶庴棪冊傪媍榑偟偰偒偨偑丄偙偺俀弨埵宯偱偼捠忢儗乕僓敪怳偵昁梫側
斀揮暘晍傪婲偙偡偙偲偼偱偒偢丄儗乕僓敪怳偟側偄丅崱擔偱偼條乆側暘栰偱儗乕僓傪梡偄偨壢妛偑敪揥偟偰偍傝
偦偺儗乕僓偵娭偟偰柍抦偱偁傞偙偲偼嫋偝傟側偔側偭偰偒偰偄傞丅偦偙偱丄偙偙偐傜偼偦偺儗乕僓偵娭偟偰徻偟偔媍榑偟偰偄偙偆偲巚偆丅
榖偺棳傟偲偟偰偼
嘆帺慠曻弌偲桿摫曻弌偵娭偟偰検巕揑側帇揰偐傜偺愢柧
嘇儗乕僓敪怳偵昁梫側嫟怳婍偲偼丠
嘊偦偟偰儗乕僓敪怳忦審偲偼丠
嘋偝傜偵恑傔偰攇摦曽掱幃偲儗乕僓棟榑偐傜尒偊傞儗乕僓偺惈幙
嘍偝傑偞傑側儗乕僓偺庬椶
偺俆杮棫偰偱儗乕僓偵娭偟偰愢柧偟傛偆偲巚偆丅
帺慠曻弌仌桿摫媧廂仌桿摫曻弌
帺慠曻弌偲偼丄忋偺弨埵偐傜壓偺弨埵偵尨巕忬懺偑娚榓偟偨帪偵丄師偵愢柧偡傞傛偆偵?冎偵憡摉偡傞侾偮偺岝巕傪曻弌偡傞尰徾傪偄偆丅
傑偢偼丄崱傑偱埖偭偰偒偨憃嬌巕儌乕儊儞僩憡屳嶌梡偑偁傞帪偵丄偳偺掱搙妋棪偱忋偺弨埵偐傜壓偺弨埵傊娚榓偡傞偺偐傪弎傋傞丅
検巕椡妛揑偵俀弨埵尨巕偺倕丄倗弨埵娫偵憃嬌巕儌乕儊儞僩偑懚嵼偡傞偲偒
偱婰嵹偝傟傞憡屳嶌梡僴儈儖僩僯傾儞偑偁偭偨丅偙傟偺揹応傪検巕壔偟偨偲偒偺昞幃偱彂偒側偍偡偲
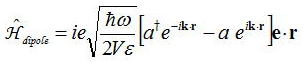
偲側傞乮埵憡崁倕(倝冎倲)偼徣偄偰偄傞乯丅偙偺傛偆側帪娫埶懚偺愛摦僴儈儖僩僯傾儞偑偁傞帪偺宯偺慗堏妋棪偼
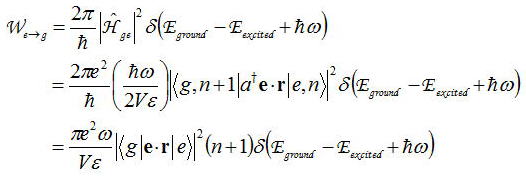
偲側傞丅忋婰偼擇偮偺崁偵暘偗偰峫偊傞偙偲偑偱偒傞丅偮傑傝丄
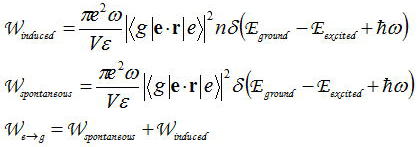
忋婰偼慗堏妋棪傪擇偮偺崁偵暘偗偰峫偊偰偄傞偑丄Winduced偺慗堏妋棪偼応偵偁傞岝巕悢偑値屄偺偲偒偵偦傟偵斾椺偟偰
椼婲忬懺倕偐傜婎掙忬懺倗傊偺慗堏偑婲偙傝傗偡偔側傞偙偲傪堄枴偡傞丅偮傑傝丄岝偑嫮偄傎偳壓偺弨埵偵桿摫偝傟偰娚榓偡傞偺偱
桿摫曻弌偲屇偽傟傞丅擇偮栚偺崁偼応偺岝巕悢偵娭學側偔慗堏偑婲偙傝娚榓偡傞偨傔帺慠曻弌偲偄偆丅
偝傜偵拲栚偡傋偒揰偼忋婰偺慗堏妋棪倂倕仺倗偼乥倕丄値亜偺検巕忬懺偮傑傝値屄岝巕悢傪帩偮検巕応偐傜乥倗丄値亄侾亜偺検巕忬懺
偮傑傝乮値亄侾乯屄偺岝巕悢傪帩偮検巕応傊偺傒崁偑懚嵼偡傞偺偱丄椼婲忬懺倕偐傜婎掙忬懺倗傊娚榓偡傞偲偒偵偼
応偵侾偮偩偗岝巕傪曻弌偟偰娚榓偡傞偙偲傪堄枴偡傞丅
師偵慡攇悢嬻娫偱偳偺掱搙偺帺慠曻弌偺慗堏妋棪偑婲偙傞偺偐傪媍榑偟偰傒傛偆丅
忋幃傪慡攇悢嬻娫偱榓傪偲傞丅冎亖冎乮倠乯偲攇悢偵埶懚偡傞偺偱丄
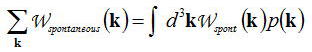
偲側傝倫乮倠乯偼儌乕僪枾搙偱偁傞偮傑傝
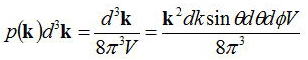
偱偁傞丅傛偭偰丄帺慠曻弌崁傪慡攇悢嬻娫偱榓傪偲偭偨抣偼
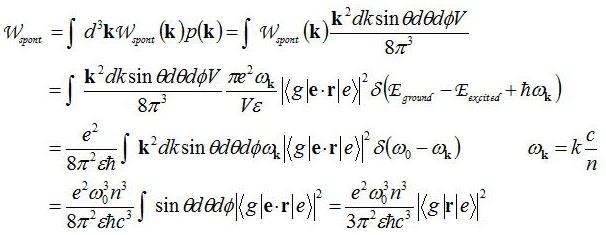
偲側傞丅偙偺抣偺堄枴偼扨埵帪娫摉偨傝偵偳偺掱搙偺妋棪偱帺慠曻弌偑婲偙傞偺偐傪帵偟偰偄傞丅
傛偭偰丄椼婲弨埵偵N屄偺尨巕偑扨埵懱愊摉偨傝懚嵼偟偨偲偡傞偲丄偦偺懱愊偐傜岝巕偑曻弌偝傟傞妋棪偼N*Wspont偱偁傞丅
偙偺Wspont偺抣乮學悢乯傪傾僀儞僔儏僞僀儞A學悢偲屇傇偙偲傕偁傞丅
