---

自然放出＆誘導吸収＆誘導放出

次に前節で述べた誘導放出の項に関して議論していく。

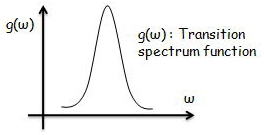
一般的に遷移δ（Eｇound−Eexcited＋?ω）は不均一広がりがあり、スペクトル広がり関数ｇ（ω）を考えて議論していく必要がある。



誘導放出の遷移確率は以下のようになる。



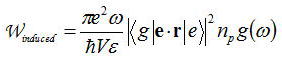
ここでモードがωの光強度Iω



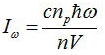
を用いて上式を整理しなおして



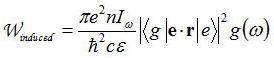
また、アインシュタインのB係数を用いると、



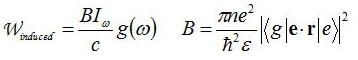
上式は１原子に関して計算した結果であるが、励起準位にNｅ個の原子があるとすると、上式にＮｅをかけた値が遷移確率となる。

さらに上式は誘導放出に関しての結果であるが、同時に誘導吸収も起こる。

誘導吸収とは場に光子があるときにその光子を１つ吸収して基底状態から励起状態に遷移することを意味するが、

誘導吸収の遷移確率も上式と同じになる。そのため、誘導放出と誘導吸収を合わせて考えると、放出から吸収を引いた正味の放出は

単位体積あたり



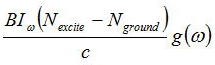
となる。正味の誘導放出はＮｅ−Ｎｇ＞０のときにおこることを上記の式は示している。

逆にＮｅ−Ｎｇ＜０であるときは誘導吸収となる。誘導放出を起こしてレーザを作るためには、励起準位の分布を

基底準位よりも分布を大きくする必要がある。通常はボルツマン分布をしているためＮｅ−Ng＜０となるため、基本的には誘導吸収が起こる。

Ｎｅ−Ｎｇ＞０にする、つまり熱平衡分布と逆の分布である反転分布を起こすためには汲み上げの操作をポンピングを行う必要がある。

ポンピングの方法はのちの節に述べるとして、誘導放出によって光がすすむ時間ｔ＋ｄｔの間に光強度がｄＩ（ｔ）だけ増加すると



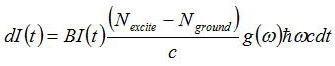
だけ光強度が増幅される。時間ｔ＋ｄｔの間に移動する距離はｚ＋ｄｚまで進むので、



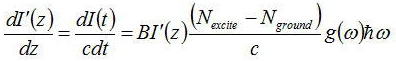
従ってこの微分方程式を解くと、



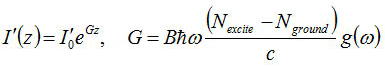
のように変化する。ｅ(Gz)はパワーの利得（Ｇａｉｎ：ゲイン）、Ｇは利得定数と呼ばれる。