---

前節までは、Laser発振に関していろいろと発振条件や反転分布、共振器の役割等を説明してきて基本的な概念はつかめたと思うが、

やはり、一度はより一般的な波動方程式からきちんと導いておくことに意味があると思う。

以前電磁場の量子化のときに位置演算子ｑと運動量演算子ｐを用いて、消滅生成演算子ａ、ａ†を定義して電磁場量子化したと思う。

ここでは電場をａ，ａ†を用いて計算せずに、ｐ、ｑを用いて議論していく。ｐ、ｑを用いた電磁場は



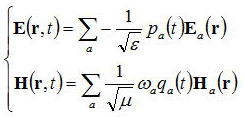
であり、



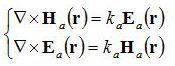
共振器にはレーザ媒質が含まれておりそこで発生する時間に依存する分極Ｐlaserと共振器に関係なくその誘電率εが

時間に依存しない分極Ｐnonresonantがある。



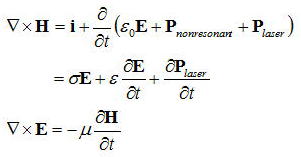
σは実効的な伝導率で共振器でのロスを表現するために導入している。



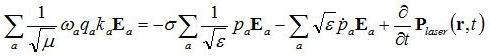
これにＥｌ（ｒ、ｔ）をかけて共振器内を積分すると、ここでは証明しないが直交条件がある∫ｄＶＥａＥｌ＝δａｌを用いて整理すると、



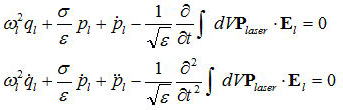
さらに下記の条件を用いて上式を整理してみると



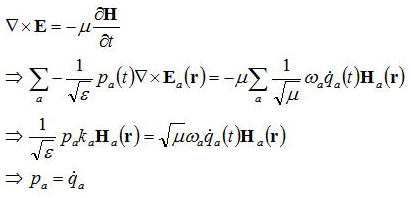
なので、



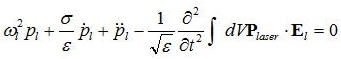
となる。第四項が０だとしたときに上式の解は、



ε/σは減衰時間を意味するが、実際の共振器がロスが小さく長い減衰時間であることを考えると、



として、pl0(t)の時間変化は非常にゆっくりである、つまり長い減衰時間であると考えると、



であり、２階微分項は非常に小さいとする。



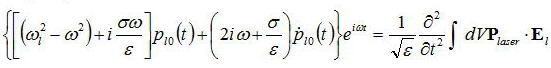
で分極Pは以下のようにかけるので



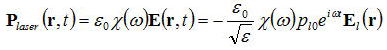
を代入して、定常状態ｐの一階微分が０とすると、



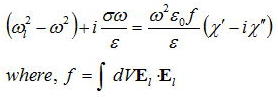
である。上式はレーザ発振条件の一般的な形式であり、前回導いた簡略したレーザ発振条件をも包括する形である。