---

光子数状態

エネルギーにはある最低値があるはずである。これをＥ０としてその状態を|０>と表す。

それより、高い固有値と固有状態をＥｎと|ｎ>とする。その固有状態に演算子したときに以下の関係が成り立つと仮定してみる。



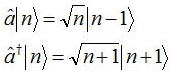
これを用いて以下の計算をしてみる。



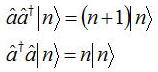
よって交換関係を計算すると



となる。このことは上記の仮定の下で交換関係が成立していることが分かる。さらに、エネルギーＨを計算してみる。



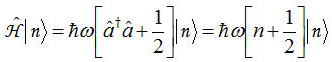
となる。したがって、エネルギーＥは?ωごとにステップ状になっている。この?ωのエネルギーごとに１つの光子が発生し

エネルギーが増加していると考える。上記の状態ではｎ個の光子があるとしてｎ光子数状態と呼び｜ｎ＞で記述する。

｜０＞を真空状態または真空という。またa†aの固有値は光子数を与えるので、



を光子数演算子という。

さらに上記の仮定をみるとａとａ†はそれぞれ光子を消滅させたり生成したりするので、消滅演算子、生成演算子という。


電場の揺らぎ

次に電場の期待値は電場演算子を用いると、



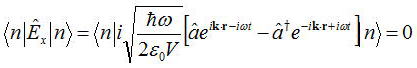
である。これは、ａとａ†の位相がそろっていないために平均すると０になると解釈され、電場振幅が０を意味するわけではない

実際、光子数ｎと位相φとの間には不確定性関係、



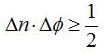
があり、光子数ｎが決まると、その位相は不定になる。つまり上式の期待値は光子数が決まっておりその期待値をとった際に

電場の位相が定まっていないことを意味している。

次に、電場の二乗の期待値を計算すると、



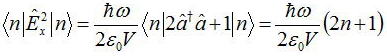
となり、ゼロでない。またこれより電場の揺らぎを求めると、



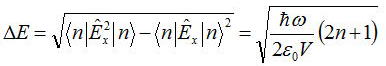
となる。これを電場の揺らぎによるものである。さらにｎ＝０であっても電場の揺らぎは残っている。この揺らぎを真空の揺らぎ

といい、電磁場を量子化したときに出てくる興味深い現象である。