---

コヒーレント状態

電磁場の量子化によって光子数状態という量子状態を表現してきた。それによって光の粒子的な側面を見てきたわけだが

量子力学において古典電磁気学のような波動的な特徴を表すこともできないといけない。

そのような量子状態をコヒーレント状態と呼び、レーザ光がその状態を表す代表格である。

　光子数状態｜ｎ＞は完全系をなすから、任意の複素数αを用いて次の量子状態を考える。



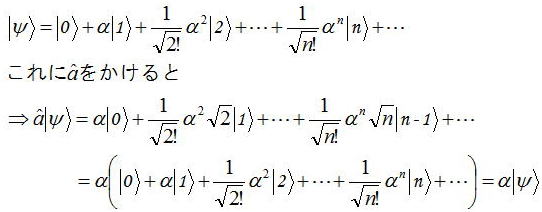
となる。よって｜ψ＞がａの固有状態でαが固有値になっている。そこで規格化を行って、



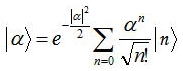
という量子状態を考える。この状態をコヒーレント状態という。さらに消滅演算子ａをかけると、やはり



が成立する。では電場の期待値が古典的な波動的な性質を表すのかどうかを見てみる。

コヒーレント状態の電場の期待値を計算すると、



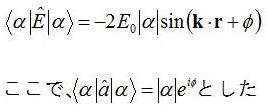
が成立する。よって、コヒーレント状態の電場の期待値が正弦波であらわされる古典的な電磁場に対応する

量子力学的表現になっている。

コヒーレント状態の各光子数状態のまえの係数の二乗はポアソン分布となっており、



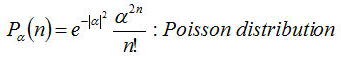
発振しきい値以上のレーザ光の光子数分布に等しい。つぎにポアソン分布の例を示す。



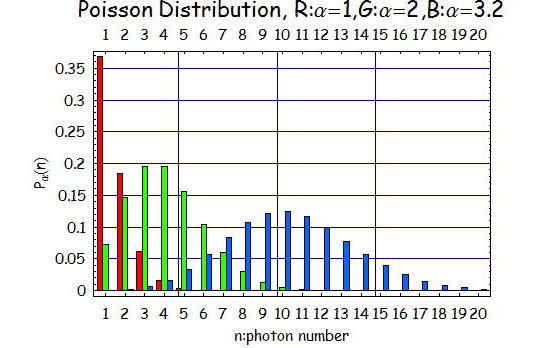
電場成分が揺らぎ成分を含めてどのようなふるまいをするのかを一度図にしてみるのはイメージを作る上で重要である

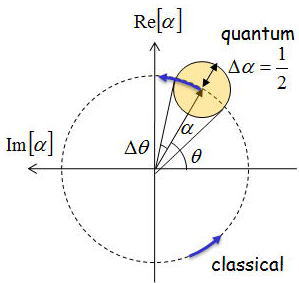
厳密な証明はしないが電場成分を実数部と虚数部に分けた際に、古典論では点線上をωｔの角速度で回転し、その実部への

射影成分が振幅で位相成分が実軸からのなす角であった。しかしながら、量子論では下の図に示したように振幅と位相に

ほぼ円形＊の不確定性があるために時間ｔを指定して角速度ωｔを指定しても、電場と位相は一意に決まらず、

ある揺らぎをもっていることになる。

（＊）現状のところ光子数演算子に共役な位相演算子が存在しないため円かどうかが分かっていない



実際に平均光子数とその揺らぎを計算すると、



であり、上式の前者を微分すると、



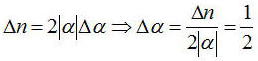
となる。位相成分は演算子がないために計算はできないが、円形に近い揺らぎと考えられている。

このコヒーレント状態の電場振幅と位相の揺らぎを時間軸で表現したのが、下のグラフである。（振幅=3,100のとき）



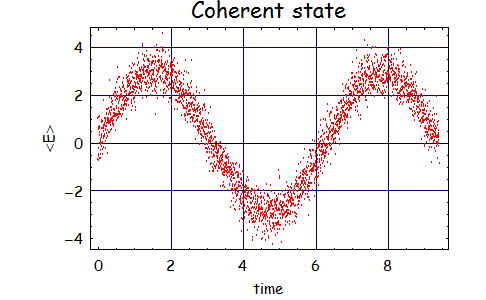
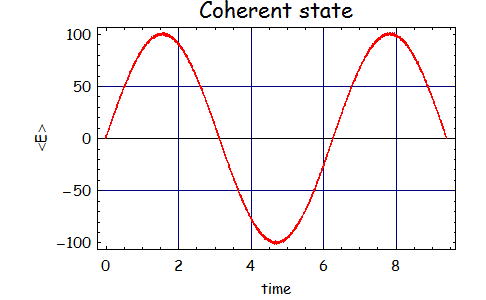
上での議論と併せて考えると、振幅と位相揺らぎはほぼ真空でもかかわらず一定（１/２）の揺らぎを持っているため、

振幅の期待値＜α＞を大きくしていくほど振幅に対して揺らぎの影響が小さくなっていることが見て取れる。