---

電気双極子相互作用

光電場



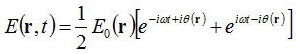
に対して、電気双極子相互作用



を考える。ここで、ｅは単位偏光ベクトルである。伝搬光の場合、位置に依存した位相は、



と表される。ここで下の図に示すようにｑを電荷として、原子中の正負の電荷が分離して電気双極子モーメントができる。

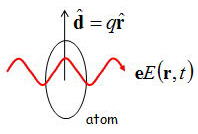
量子力学的に電子双極子モーメントの大きさを求めると、電気双極子モーメントの電場ｅ方向への射影をとり、

その非対角行列要素は



となる。対角成分に関しては、原子の波動関数はψi(i=e,g)は原子の対称性のため偶関数か奇関数であり、

電気双極子モーメント演算子がと奇関数でため、対角成分のr|ψi|^2(i=e,g)の積分は必ず０になるので

電気双極子モーメントの対角成分は考えない。

また、非対角成分であっても

基底状態と励起状態の波動関数がそれぞれ偶奇が異なっていないと電気双極子モーメントは発生しないことに注意したい。

よって前節で導いたシュレディンガー方程式は非対角成分のみを考えて、



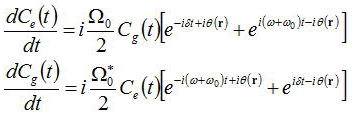
ここでラビ角周波数、と角周波数離調

　　　　　

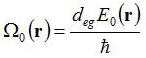
を導入した。

上式でω＋ω０で速く振動する項を無視する回転波近似を用いると

（速く振動する項は最終的に検出する際に、光の角周波数程度の高速検出するディテクタはないので平均化され０となるという近似）



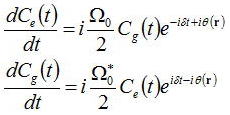
となる。Ｃｇ、Ｃｅに関して初期条件Ｃｇ（０）＝1，Ｃｅ（０）＝１として解を計算すると、



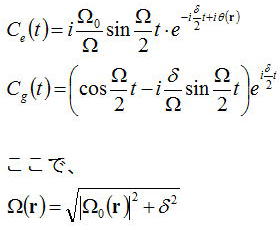
まだ説明していなかったが、量子力学上｜Ｃｇ｜＾２と｜Ｃｅ｜＾２はそれぞれ励起状態と基底状態の占有確率を与える。その間には



の関係が成り立つ。そこで、励起状態と基底状態との間を時間的にどのように占有確率が変動しているのかを下の図に示す。



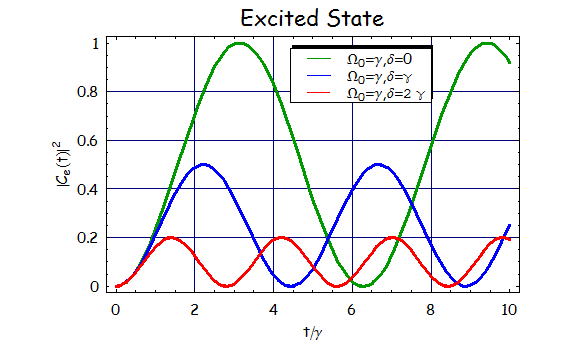
以下の励起状態と基底状態の差（反転分布）という観点で計算してみると、



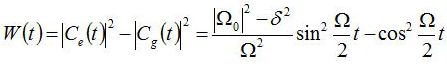
となる。