---

密度行列（緩和がない場合）


前節では１原子における２準位原子系における励起状態と基底状態の存在確率に関して理論的に取り扱ってきた。

この節ではシュレディンガー方程式を密度行列に書きなおすことで、自然放出による２準位原子系の緩和の効果を取り入れられる

また、多原子に関して統計的な取り扱いをすることができるメリットがあるため、それに関して議論していくことにする。

まず、２準位１原子系のシュレディンガー方程式を復習すると、

ハミルトニアンが原子の効果のみで光の影響がなかったとすると、Hatomを用いて



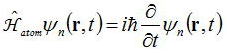
とすると時間を含まないハミルトニアンHatomの固有関数φn（r）を用いて



となる。一般解はその線形結合となるので、



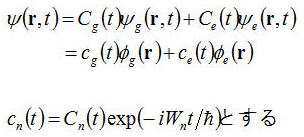
ここでｃｎ（ｔ）の意味は時間変化をふくめた確率振幅である。

では次に光の影響である電気双極子相互作用Ｈdipなどを含む一般的の場合、



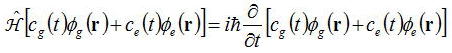
となる。ここで、φａ＊を左からかけて体積積分し、Ｈの行列要素、



を用いて確率振幅ｃｎ（ｔ）に関する運動方程式を整理すると、励起状態と基底状態それぞれに対して



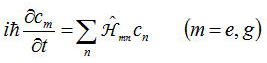
が成立する。ここまでの話は前節までに考察してきた。さてさらにここから考えを進めて、１原子から多原子への展開を考える。

単位体積中にN個の原子があるとする。i番目の原子の確率振幅をciaとcibとして次式の密度行列ρ（ｒ、ｔ）を定義する。



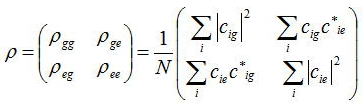
対角行列は各順位の分布確率を表し、対角成分の和をとると１が成り立つ。

さらに、非対角成分は巨視的な双極子モーメントを定量化するときに用いられる。

密度行列を考えるにあたりメリットは、純粋状態つまり個々の原子の確率振幅ｃiaとｃibがわからなくても、

巨視的な多数の原子集団の統計的な量（状態：混合状態という）｜ｃia｜^2やciacib*などを用いれば、

実験から得られる量を定量的に扱える点が密度行列を導入するメリットである。

では、上式の密度行列と先ほど導いた純粋状態の運動方程式と密度行列を用いて混合状態で成立する方程式を導くことにしよう。



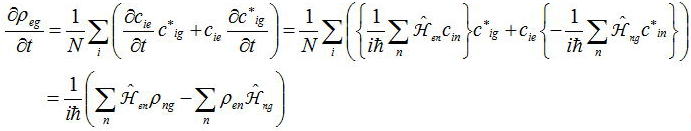
となり、交換子[A,B]=AB-BAを用いて表すと、



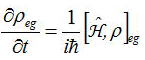
となる。

一般的に密度行列の各成分は上式の関係が成立するので、密度行列の運動方程式は以下のように記述される。



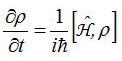
以上より、非常に難しく思われた、多原子系で（今回は２準位系だが、一般的には多準位系でも成立する）成立する運動方程式は

上式のように密度行列を導入することでシンプルな形で表現できることが分かった。

上式は各準位間での緩和過程が取り込まれていないがそれに関しては次節で議論することにしよう。