---

密度行列（緩和過程がある場合）


さて、緩和過程がない場合の密度行列（多原子系において成立する運動方程式）に関して議論してきたが、

現実は各準位間に高エネルギー準位から低エネルギー準位への緩和（高エネルギー準位のpopulation減少：分布確率の減少）

という過程がある。ここでは、それを取り込んだときにどのような運動方程式になり、そこから見える巨視的な物質の性質は何かを

考察していくことにする。

前節で導いた緩和過程がない場合の密度行列についての運動方程式は



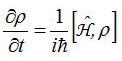
であった。上式は各密度行列ρ（ｒ、ｔ）の成分に対して成立する。

さらにこの方程式を具体化するために、ハミルトニアンHの各成分に関して議論を進めると、

固有エネルギーWnを?Ωｎと書くと準位ｅ、ｇ間の遷移に伴って吸収放出される遷移周波数は、



となり、また、各ハミルトニアンＨの行列要素次のように書かれる。原子の固有関数におけるハミルトニアンＨａｔｏｍにおいて



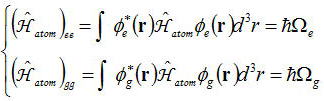
と対角成分のみとなり、非対角成分はゼロとなる。つぎに電気双極子相互作用ハミルトニアンＨdipoleは



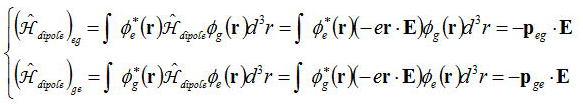
となる。このように電気双極子相互作用により非対角成分があるため、密度行列の運動方程式において

ポピュレーションの変化つまり励起現象：遷移現象が起こる。そこで、密度行列の運動方程式の非対角成分に関して具体化すると





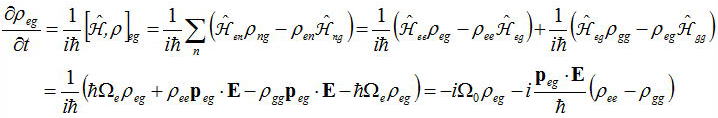
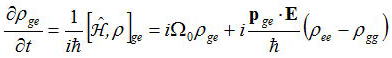
上式は非対角成分を持つために光の影響によって原子のｅ，ｇ準位間にどのように遷移行列の要素ρｅｇ、ρｇｅができるかを表している。

つまり電子双極子モーメントｐと電場Ｅに比例して、（ρｅｅ−ρｇｇ）のポピュレーションの差に比例した光の相互作用の強さにより

ρｅｇ、ρｇｅが生成されると考えてよい。

ところで、基底状態にいる原子から位相のそろった光が入射すると位相がそろいρの非対角成分ρｅｇ、ρｇｅが増加する。しかし、現実的には

初期状態から電場が自然放出や原子衝突などにより位相が変わってCieCig*の積の集団としての和の値が小さくなる。

そのため、ρｅｇ、ρｇｅは基本的にはゼロに戻ろうとする何らかの項を上式に取り込む必要がある。

この緩和の速さをγ（緩和定数）としたときに上式に現象論的に取り入れられる減衰項は、



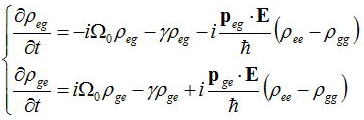
とする。γの値は原子系の複雑な衝突等の運動の結果からえられるもので、厳密な計算は困難である。しかし、いずれにしても

このような減衰定数はでてくるので導出はあるらしいがここでは行わない。

上記で説明したことを図で表したのが下の図である。



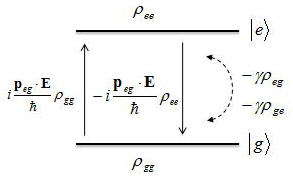
光の入射光ＥがΩ０に近いωを持っているとすると、上式の第一項がρｅｇはｅｘｐ（−ｉΩ0ｔ）という解をもっているのが分かるので、

ρｅｇはωで強制振動をうける。そこで、



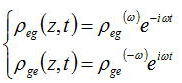
と表す。光電場を周波数ωと波数ｋに関してフーリエ展開して、



と表し、これを上式に代入すると、



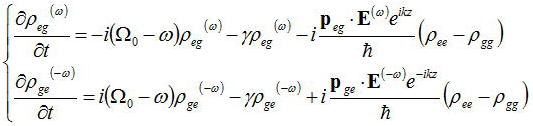
が得られる。上式において電場の片方の周波数成分しか含ませないのは、光の２倍の周波数で変化する項が出てくるので

そのような変化はディテクターで検知できないので省く。上式の近似を回転波近似という。