
揹婥姶庴棪乮慄宍姶庴棪乯丗枾搙峴楍曽掱幃偵偍偗傞掕忢夝
擖幩岝嫮搙偑堦掕偱丄娚榓帪娫乮侾/兞乯傛傝廫暘帪娫偑偨偭偨屻偱偼丄慜愡偺枾搙峴楍曽掱幃偺塃曈偺帪娫曄壔偼傎傏侽偵嬤偯偔
掕忢忬懺偵側偭偰偄傞偲峫偊傜傟傞丅偝傜偵丄庛偄岝嫮搙偺応崌偵偼偡傋偰偺尨巕偼傎偲傫偳摦偐側偄偨傔丄婎掙忬懺偵偄傞偲峫偊傜傟傞
偮傑傝兿倕倕亖侽丄兿倗倗亖侾偲嬤帡偡傞偙偲偑偱偒傞丅掕忢夝偼丄
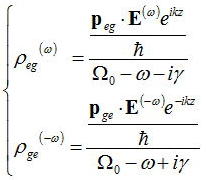
傪摼傞丅偙傟傪梡偄偰岝擖幩偵傛偭偰偱偒傞扨埵懱愊摉偨傝俶屄偺尨巕偺宯慡懱偵傛傞嫄帇揑憃嬌巕儌乕儊儞僩偺婜懸抣傪
媮傔傞偙偲偑偱偒傞丅廳偹崌傢偣忬懺冇偵偍偗傞偦偺婜懸抣偼丄
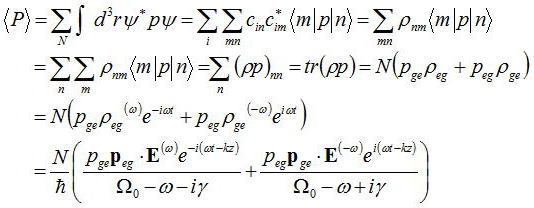
N偼扨埵懱愊拞偺尨巕悢偱偁傞丅E偲摨條偵P傕僼乕儕僄暘夝偡傞偲
偲側傝丄憃嬌巕儌乕儊儞僩傪揹応偵斾椺偡傞崁偲峫偊偰丄
偲揹婥姶庴棪乮electric susceptibility乯:冊偺斾椺學悢傪梡偄傞偲丄偦偺揹婥姶庴棪偼
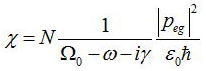
偱偁傞偙偲偑暘偐傞丅忋幃傪幚悢晹暘偲嫊悢晹暘偵暘妱偟偰寁嶼偡傞偲
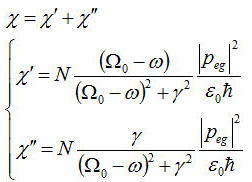
偲側傞丅冎偺娭悢偲偟偰忋幃傪恾帵偡傞偲丄
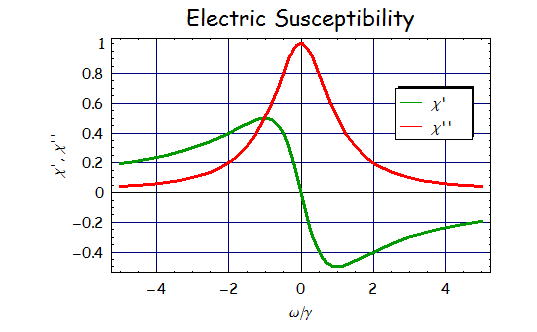
揹婥姶庴棪偺攇挿埶懚惈偼孅愜棪偺暘嶶偲娭學偟偰偄傞偺偱丄暘嶶嬋慄偲屇偽傟偰偄傞丅
摿偵丄幚晹冊乫偼孅愜棪偵丄嫊晹冊乭偼媧廂偵娭學偟偰偍傝丄
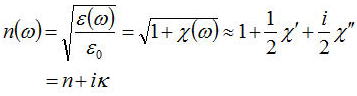
偲偄偆娭學偱偁傞
孅愜棪偑冊乫偵懳墳偟偰偄傞偙偲傪峫偊傞偲媧廂嬤朤埲奜偺廃攇悢偵偍偄偰丄冎偑崅廃攇乮偮傑傝抁攇挿乯偵峴偔傎偳塃尐忋偑傝偱偁傞
偙傟傪惓忢暘嶶偲偄偆丅偟偐偟側偑傜媧廂嬤朤偱偼崅廃攇偵峴偔傎偳塃尐壓偑傝偱偙傟傪堎忢暘嶶偲偄偆丅
師偵丄媧廂偵娭偟偰媍榑偡傞偲丄幚嵺偺媧廂慄偺峀偑傝偼丄忋幃偱昞尰偡傞傎偳娙扨偵兞偩偗峀偑偭偰偄傞偲峫偊傞偙偲偑偱偒側偄丅
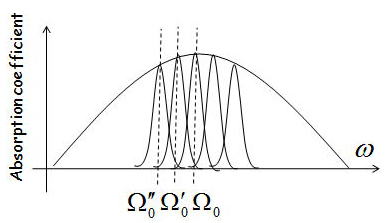
偮傑傝丄忋恾偵帵偟偨傛偆偵俀偮偺媧廂慄偺峀偑傝偺榓偱峫偊傞偙偲偑偱偒傞丅偦偺擇偮偺媧廂慄偺峀偑傝偲偼丄
嘆兌侽偩偗偺媧廂慄偵拝栚偟偨嵺偵丄兞偵憡摉偡傞媧廂慄偺峀偑傝偑偁傝丄偙傟偼帺慠曻弌傗尨巕娫偺徴撍丄僼僅僲儞
乮屌懱拞偺尨巕偺擬塣摦乯偵傛傞侾偮偺兌侽偐傜峀偑偭偨媧廂慄偱偁傝丄嬒堦峀偑傝偲偄偆
嘇媧廂慄兌侽偺暘晍偼婥懱偱偼懍搙偑暘巕傗尨巕偱堎側傞偨傔丄懍偝倴偵傛傞僪僢僾儔乕僔僼僩偑惗偠丄奺尨巕偵偍偗傞媧廂嫟柭廃攇悢
偵暘晍傪帩偮偙偲偵側傞丅屌懱偱偼丄尨巕傗僀僆儞偑偝傑偞傑側尨巕攝抲偺娐嫬偺拞偵偍偐傟傞偙偲偵傛偭偰媧廂嫟柭廃攇悢兌侽偵
暘晍傪帩偮丅偙傟偵傛傞嫟柭廃攇悢兌侽偺廤崌偟偰傞偙偲偵傛傞峀偑傝傪丄晄嬒堦峀偑傝偲偄偆
