この節で扱うのは時間に依存した摂動論を扱うことにする。
シュレディンガー方程式で厳密に解けるハミルトニアンがあり、これに微小なハミルトニアンの時間変化を与えたときに(これは実際解こうと思っても複雑すぎて解けない)、どのようにこの近似解を求めるかを扱うのが、時間に依存した摂動論である。
まず、ハミルトニアンを厳密に解ける部分とそうでない部分とに分けてみる。
ハミルトニアンの中の第一項は厳密に解けるほうであり、第二項のほうは微少量のほうである。
ここでハミルトニアンを以下のように書き換えてみる。
![]()
λの次数ごとに式は成立するはずなので、次数ごとの方程式を求めることができる。それらの式は、
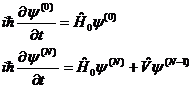
0次(上の式)の式は単なる時間に依存しないシュレディンガー方程式であり、厳密に解を求めることができる。それなので最初にgrand state(適当な状態)にいるとすると、この解は以下のように書き換わる。
次に、0次以降の解を考えてみる。つまり下の方程式についてだ。
N次の波動関数を厳密解の完全系で展開することを考える。
ここで何を目的にしているのかというと、係数であるaを決定することにある。
この式を代入して整理をしてみると、
計算は省略した。一応言葉で補っておく。まず、代入した後で左から固有関数mの状態のものを掛ける。これと直交するものは消え、mの状態のもののみが残る。最後に時間で両辺を積分していただければよい。
実はこれで基本的には、もうおしまいなのである。どこがだよって、御思いの方もいましょうが・・・
というのは、波動関数の形(任意の状態の形)がわかってしまったからだ。(当然それが計算できるかどうかはまた別の問題であるが)。つまり、求めたかったそれぞれの次数での波動関数の係数を漸化式の形ではあるが次々と求めていけるのである。後はこれをどう利用するかにすべては集約される。これに関して少し練習が必要だろう。簡単な例は教科書などで練習を詰まれるとよい。機会があればなるたけ面白い例を載せたいと思う。だけど時間がないんだよね〜〜。
少し、非線形光学のところで扱うので参考にしてみてくれぃ。
