３．１　　はじめに

系統誤差があるないにかかわらず、偶然誤差は必ず入ってくる。

では、系統誤差がない場合、ｎ回測定して、平均値　x　を求めたとする。

この平均値　ｘ　は真の値　Ｘ　ではないことは理解できるだろう。

つまり、真の値からずれたｎ回の測定値の和を平均した x の値が平均化の作業だけで、真の値　Ｘ　に

等しくはならない。（よほどの運がよくない限り）

では、平均値が真の値に近い数値になるという考えは、どういうことなのだろうか？


次の二つのシチュエーションを考える。

（a）測定値のばらつきが小さいときに求められる平均値 x
（b）測定値のばらつきが大きいときに求められる平均値 x



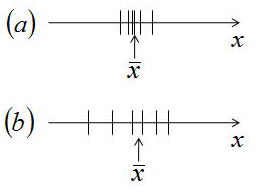
上記の測定試行回数は同じとする場合、通常（a）のほうが真の値 X に近いに違いないと考える。

では、どうすれば、この考えが正しいといえるのだろうか？

先ほどの節に述べたように、真の値　X が平均値 x を中心としたある誤差内にあることに

関しては議論できる。よって、平均値　x　は真の値　X にどれほど近い値をとると期待できるか

と考えることで、どちらの結果がより正しいと考えてよいか？という疑問を解決することになる。



３．２　　測定値の集合と平均値

物理量をn回続けて測定した値を　　x1, x2, x3, x4, ・・・・・・,xｎ　　と表す。

平均値は、以下の式となる



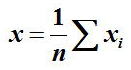
しかし、この計算のみでは平均値　ｘ　が真の値　X　にどの程度近いのかを評価することができない

そのため、測定値のばらつきの度合いを評価する尺度を考える必要がある

この尺度を考えるために分布という概念が必要になる



３．３　　測定値の分布と分布関数

実験回数はｎ回と限られた回数であるが、この回数をN回と仮想的に非常に大きな回数の測定を

行ったと仮定する、この測定値の集合体を分布（distribution）とよぶ。

これからの議論の基本となる概念は

「測定値は、このN回の測定値の分布の中からランダムにｎ個の数値を抽出した値とみなす」

という点である

N回の測定値の分布と考えると、回数Nによって縦軸が変わってしまうのは何かと面倒である

そのため、縦軸をNで割って規格化した分布関数（distribution function）を用いたほうがよい

つまり、ある測定値（あるｘ軸の値）が、測定値全体の

どのくらいの割合で含まれているかを表す関数　ｆ（ｘ）：分布関数（distribution function）　を用いる

　　　　　

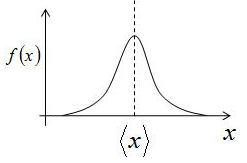
分布関数ｆ（ｘ）は確率を表すので、すべてを合わせると１になるため、



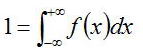
となる。

さらに、平均は先ほどの式で　xi　に　xiが起こる確率　１/n　を掛けて和をとる意味であるので、

分布関数を用いた場合は以下の式で表現できる