３．３　　個々の測定値の信頼度

次に、１回の測定値の結果が真の値　X　にどの程度近いのか、つまり、測定値の信頼度に関して議論しよう

１回の測定における値　ｘ　の誤差（真の値からの差）を



と表すことにする

この真値Xから測定値ｘがどの程度ばらついているのかを定量的に評価しようとした際に

分布関数　ｆ（ｘ）を用いて、誤差 e の二乗の値　e^2の平均を測定値のばらつき（信頼度）である

ととらえることはいい評価量であると考えられる。

式では、この量は以下で表現される



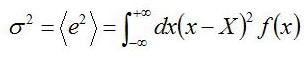
この平方根σは分布の標準偏差（standard deviation of the distribution）と呼ばれる

σ＾２は分布の分散（variance）と呼ばれる



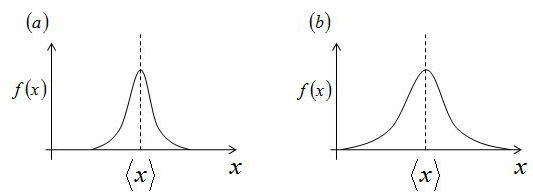
標準偏差σをばらつきの小さい（ａ）と大きい（ｂ）の場合で比較してみる。誤差　ｅ　は



であり、その二乗のｅ＾２の平均は、ばらつきが大きい（ｂ）ほど標準偏差σが大きい値を示すことは

想像に難しくないだろう

よって、標準偏差σが分布の広がり・測定値のばらつきの尺度になる。



３．４　　平均値の信頼度（標準誤差）・・・平均値からなる分布の標準偏差


個々の測定値のばらつきを表す標準偏差よりも、より精度の高い誤差の範囲を与える

標準誤差σｍの概念を導入する。通常、このσｍを測定値の誤差の評価に用いる

標準誤差σｍとは何であろうか？

例えば、ある測定を行ったとする。その時の個々の測定値　ｘ　のばらつきは、

先ほど述べたように標準偏差σで表される。

では、個々の測定をｋ回行い、その平均値＜ｘｍ＞を求める操作を考える。

この平均値＜ｘｍ＞を算出した際に、個々の測定値の組み合わせによってばらつくために

平均値＜ｘｍ＞自体も新しい分布を持つことになる。

このときの＜ｘｍ＞の標準偏差、つまり、平均値のばらつきを考える。

この平均値のばらつきが標準誤差σｍを表すことになる


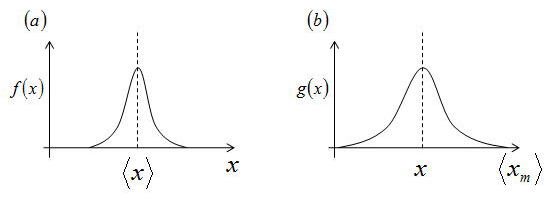
（ａ）標準偏差・・・個々の測定のばらつき
（ｂ）標準誤差・・・平均値のばらつき



３．５　　σとσｍの関係


σとσｍとの間には関係がある。それに関して説明しよう

n回測定した集合ｘ１、ｘ２、・・・・・、ｘｎにおいて、ｉ番目の測定値における誤差ｅｉは



とあらわされる。平均値＜ｘ＞の誤差Ｅは、



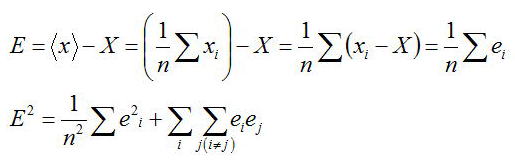
測定回数ｎを非常に大きくした際に、誤差E＾２の平均をとることを考える



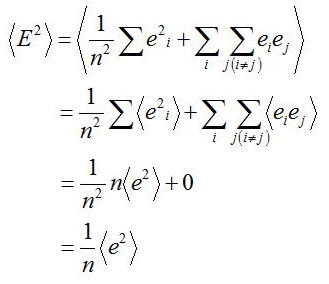
誤差ｅｉの平均＜ｅi＞はｉに依存せずに同じ値をとるので＜ｅi＞=＜e＞、

また＜ｅｉｅｊ＞は平均をとると平均値Ｘの周りで正負均等に分布すると考えているので

測定回数ｎが十分大きければ、ｅｉｅｊを打ち消すようなｅａｅｂが存在するはずである

そのため、＜ｅｉｅｊ＞＝０の関係を用いている

また、σｍ＾２＝＜Ｅ＾２＞、σ＾２＝＜ｅ＾２＞であるので、標準偏差と標準誤差との間には



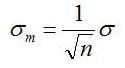
これは、何を意味しているのかというと、標準誤差σｍは標準偏差σを√ｎ倍だけ小さいばらつきであることを

意味している。つまり、ｎ回の測定から求めた平均値のばらつきは測定回数に依存することを意味している

（σは１回の測定結果のばらつきであり、装置の精度に依存するため、測定回数には依存しない）

つまり、測定回数ｎが大きいほど平均値の精度が良くなることを意味している。

しかしながら、その精度の改善率は√ｎでしか改善しない、つまり１/10に改善しようとした際に

100回も計測する必要がある。そのため、もともとの計測精度σを改善知る必要がある