３．４　　実験からσとσｍの推定する方法

（２）一般的な値ｘからの偏差

この節では以下の式



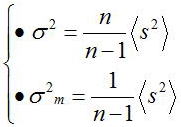
に関して考えてみる。上式は測定値＜ｘ＞からのばらつきｓの二乗平均が

真値Xからのばらつきであるσよりも小さいことを意味している

そのことは以下の点で説明できる。ある値ｘからの測定値ｘｉの偏差の二乗平均の平方根をＳ（ｘ）とすると



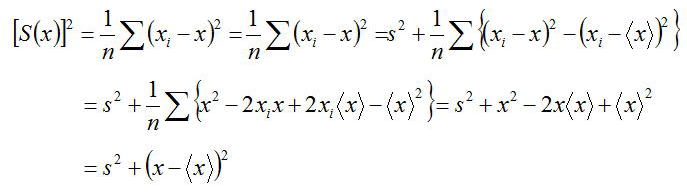
となる。

上式はある値ｘが平均値＜ｘ＞のときにばらつきが一番小さくなることを意味する

よって、真値Ｘからのばらつきσよりも測定値＜ｘ＞からのばらつきｓの二乗平均のほうが

小さくなることを意味する



３．５　　ガウス分布（Ｇａｕｓｓｉａｎ　ｄｉｓｔｒｉｂｕｔｉｏｎ）

いままで測定値の分布の形状に関しては議論してこなかったが、

この節からは、分布の形状に関しても議論していこうと思う

では、どのような分布を考えればいいだろうか、理由に関してはあとで述べることにして

ガウス分布（Ｇａｕｓｓｉａｎ　ｄｉｓｔｒｉｂｕｔｉｏｎ）　　または、　正規分布に対して議論を進めていこうと思う

ガウス分布とは



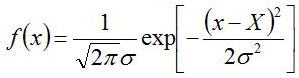
ｆ（ｘ）の指数関数の前の係数は規格化のための係数である。

さらに、標準偏差はσである。



３．６　　積分関数（Ｉｎｔｅｇｒａｌ　ｆｕｎｃｔｉｏｎ）

ｆ（ｘ）によって−ｘからｘの間に存在する測定値の割合をφ（ｘ）とすると、



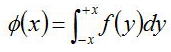
である。



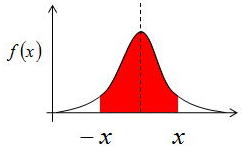
このような分布を積分関数とよぶ。｛−ｘ，ｘ｝の領域に存在する確率を下に示す



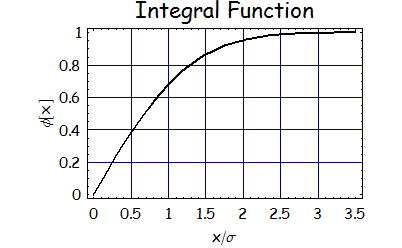
いかに、真値からσの何倍離れたときにどのくらいの存在確率になるのかを数値として示した





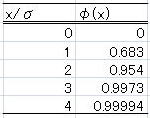
３．７　　誤差の誤差

以前に＜s^2＞をs^2で置き換えてσｍとσに関して実験値から推定して議論した。

しかしこの置き換えは十分に意味のあるものなのだろうか。この節ではその点に関して議論する。

s＾2と＜s^2＞との差は



この二乗平均をとると、



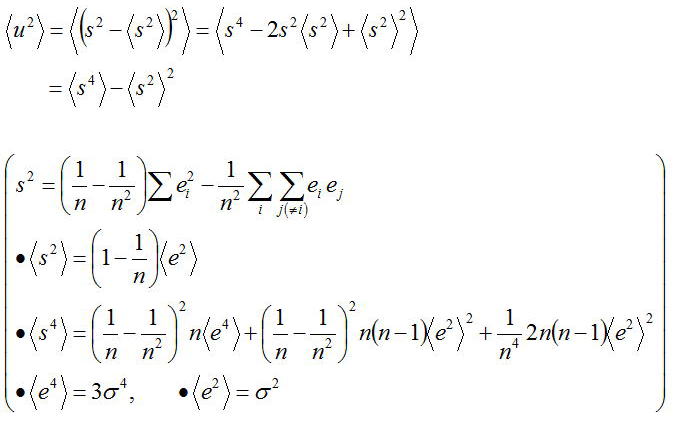
である。故に、



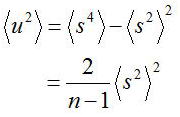
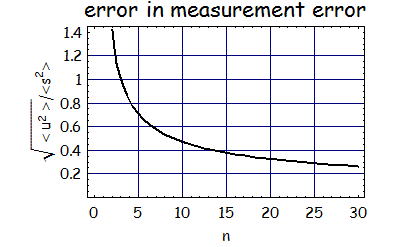
となる。以上から、＜s^2＞をs＾2に置き換えたことによる誤差は、＜u^2＞の平方根は

10回サンプリングをとることで、ばらつき量＜s^2＞の半分程度の誤差があることが分かる

つまり、実験から推定したσ＾２はその半分の値程度はばらついてしまう

さらに実験回数を増やしたとしてもその誤差の改善量は緩やかであることを理解しておく必要がある

実験から推定したσの誤差を小さくするために、実験回数を無駄に増やすことも考えられるが

実験条件を完全におなじにすることは難しいので必ずしもこれが得策ではないことを覚えておく必要がある

以上から、σを実験から推定した際にこの程度はどうしてもばらついてしまうことを理解しておく必要がある。