衝撃の中心

２．１　衝撃の中心（center of percussion）

　　　　撃力の問題で少し面白い例題があるので、少し考えてみることにしよう。
　　　　問題は何かというと、タイトルの通りに衝撃の中心（center of percussion）であるわけだが,
　　　　これが何かというと、ある剛体の点Oに瞬間的に撃力（撃力は瞬間であるわけだが）を
　　　　与えたとき、ある点O’を持っているとその衝撃を感じない点がある、さてその点は
　　　　どこでしょうという問題だ。
　　　　下に図を書いておくが、
　　　　　　　　　　　　　　　
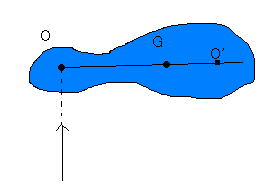
　　　　点Oに撃力（力積）が働くものとして、重心Gと点Oの直線に垂直に働くものとする。
　　　　GO間の距離をｈとし、Gはの方向にuの速度で動き始めるとする。
　　　　剛体の撃力の節（２．３）で述べた力積と方程式の関係式
　　　　重心の運動方程式より
　　　　　　　　　　　　　　　　　　　　　　
　　　　また、剛体が　の角速度で動き出すとすれば、角運動量の式より
　　　　　　　　　　　　　　　　　　　　　　

　　　　つまり、重心は　　で動き始め、剛体は重心周りに　　の角速度で回りだす。
　　　　OGの延長線上Gから距離ｘのところに点O'をとると、
　　　　　　　　　　　　　　　　　　　　　　
　　　　これは、
　　　　　　　　　　　　　　　　　　　　　　
　　　　となるから、　　のところでこの速さは０となる。
　　　　このような点は撃力の働いた直後、速度が０になっており、剛体は最初の瞬間O'の
　　　　周りに回ると考えてよい。OO'間の距離は
　　　　　　　　　　　　　　　　　　　　　　
　　　　分子はO回りの慣性モーメント　I　に等しいので、
　　　　　　　　　　　　　　　　　　　　　　
　　　　となる。
　　　　あれあれ？？これは前の物理振り子を考えるときの相等単振り子の長さに
　　　　等しいではないか！！
　　　　このとき、O'をOに対する衝撃の中心（center of percussion）という。
　　　　つまり、O'に手をもってきてOに撃力を加えても衝撃は感じない。
　　　　ほうほう、ではよく野球でバットの芯を捕らえると力が感じないというのはまんざら
　　　　うそではないようだ。
　　　　このことをもう少し次の節で議論してみよう。

２．２　バットの芯はどこにある！？
　　　　
　　　　問題を簡単にするために、ボールが衝突したとき、手からの力積分は考慮に
　　　　入れないものとする。（もし芯なら力を感じないんだから無理にリキんでバットに力を入れなくて
　　　　もいいでしょ？）
　　　　また、今回は内角に差し込まれたとしてバットを振る軸は点Oの位置にあるとする。

　　　　　　　　　　　　　　
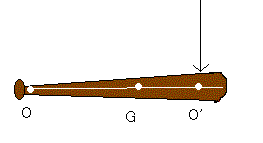
　　　　手は点Oに、ボールは重心からｈだけ離れたところにあり、O'（ボールがぶつかるところ）は
　　　　Gからｘだけのところにある。
　　　　いまこのｘがどの位置にあるのかをOに力が働かない（軸なので速さが０になる）という条件から
　　　　求めてみることにしよう。
　　　　衝突前のバットのOを軸とした角速度とする。
　　　　上と同じように、バットに対してボールがぶつかるほうを正にとり方程式を立てると、
　　　　重心の方程式は
　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　（重心の初速度がであるため）
　　　　角運動量の式は
　　　　　　　　　　　　　　　　　
　　　　これらの式から、点Oに関しての速さは　　　　　
　　　　　　　　　　　　　　　　　　
　　　　この式に上の式たちを代入すると
　　　　　　　　　　　　　　　　　　
　　　　これが０になるという条件から、
　　　　　　　　　　　　　　　　　
　　　　よってどこにボールを当てればいいかというと、
　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　
　　　　これは上で出した答えと同じになっている。
　　　　なんて偶然な、しかもこれから言えることは、バットの芯は誰が振ったとしても
　　　　軸を手の位置にしておけば、同じ位置にあるということになる。
　　　　実際腕のリーチもあるので多少位置は変わると考えられるが・・・。
　　　　それにしても、力がかからないならスムーズにバットが触れるわけだ（ナットク、なっとく）