---

スクイーズド状態

光のコヒーレント状態に関して議論してきたが、もうひとつ重要な状態としてスクイーズド状態（Squeezed state）がある。

スクイーズド（Squeezed）とは”圧搾された”という意味で、何が圧搾されたのかというと、位相と振幅の揺らぎの量がコヒーレント状態から

圧搾されたという意味である。位相と振幅の揺らぎは前節でみたように円形の揺らぎを持っていたが、この量を縮退したパラメトリック

増幅器を使うことによってその揺らぎを不確定性関係を損なわない範囲で制御することが可能である。

このことをもう少し詳しく説明しよう。

縮退したパラメトリック増幅器とは、非線形光学で説明した角周波数ω３のポンプ光から角周波数ω１の信号光を入射して

増幅し、さらに縮退なのでω２＝ω３−ω１＝ω１となるような副産物の光（アイドラー光）を生成する増幅器のことである。



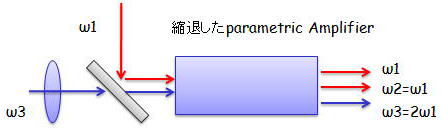
このような増幅器を通した際に、生成される電場Eω１とEω2の大きさは、それぞれ、



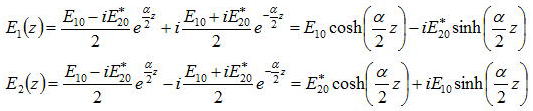
であった。（参照：非線形光学）

そこで上式の類推から入射光ａと出射光ｂの間で以下の関係があると考える。



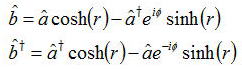
上式のｒ、φの意味は後で明らかになるが、まずは、交換関係が変換光に対しても成立するか見てみよう。



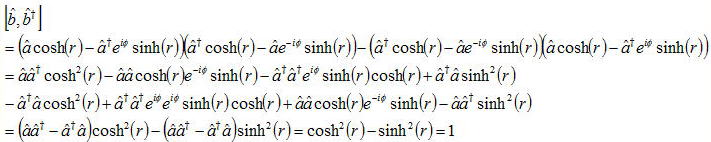
となり交換関係を満たす。このように交換関係を満たすため、演算子ｎ＝ａ†ａの光子数状態｜ｎ＞と対応させた



とすると演算子ｂの固有状態｜β＞ｇとすれば、コヒーレント状態｜α＞に対応した



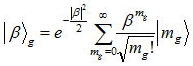
となる。ここで一般的な｜β＞ｇを｜ｎ＞で展開できれば光子数と対応が取れてイメージがしやすいのだが

非常に複雑なため、ここでは実験的に意味のあるβ＝０の状態・・・・・「スクイーズされた真空場」についてのみ説明をする

|β＝０＞ｇを｜ｎ＞で展開したときの展開係数＜ｎ｜β＝０＞ｇは以下のようになる。



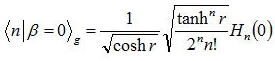
ここでHn（０）はエルミート多項式である。より具体的に|β＝０＞ｇを展開すると



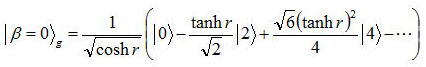
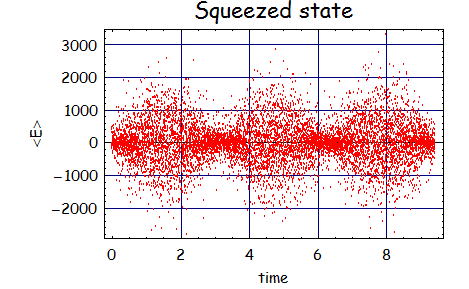
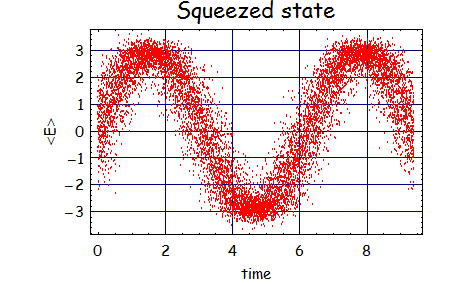
この式からわかるようにスクイーズされた真空場は、偶数個の光子流である。

このときの光子数分布は明らかにポアソン分布となっていないので、光子間に「相関」があるといえる。

スクイーズドされた真空場に関して多少明らかになってきたところで、スクイーズドと呼ばれている理由を見ていこう。

演算子ｂで使われている消滅・生成演算子ａ、ａ†を実部と虚部で分ける演算子ｘ１、ｘ２を用いて書きなおしてみると、



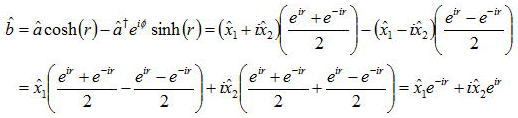
これの実部と虚部の演算子の期待値と分散を計算すると、



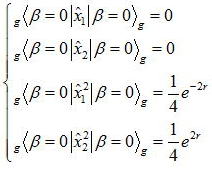
従って、量子揺らぎの値を計算すると



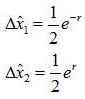
上記から明らかだと思うが最小の不確定状態であることが見て取れる。

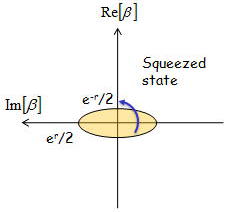
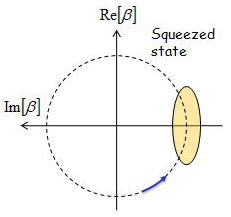
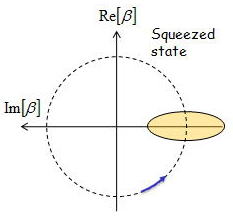
これをもとにしたスクイーズされた真空場のイメージをコヒーレント状態の真空場と比較して表現すると、



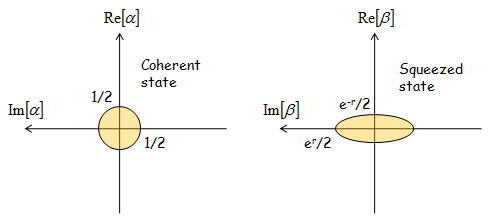
となる。ここでわかったと思うが「スクイーズされた」とは量子揺らぎのｘ１成分とｘ２成分で非対称になっていることに由来する

また、ｒをスクイージングパラメーターと呼ぶ。このパラメータは非線形結晶との類似で最初に説明したαｚ/２から実験的に決定される。

ここでは、わかりやすくするためにｘ１、ｘ２成分をスクイーズしたが他の方向からのスクイーズも

適当な位相因子を導入すれば、スクイーズすることも可能である。

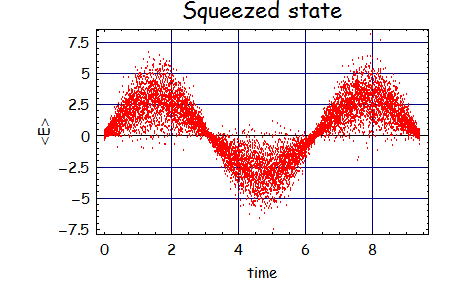
最後にいくつかのスクイーズド状態の電場のイメージを表現しようと思う。