目次
回折格子からわかる波長分解能と波長範囲
回折格子の細かい導出に関してここでは述べないが、以下のリンクから参考にして、
https://www.thepulsar.be/article/building-a-visible-spectrophotometer/
ある波長を回折格子にαの角度で入射させたときに、その波長が最も強い強度として反射角βに反射するときの数式は、
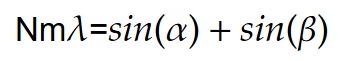
となる。m次回折光で回折格子の法線方向に対して、αとβである。
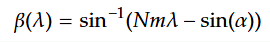
異なった波長が回折格子に入射したときに
- 回折角βがどれ程度変化するか
- その回折光をセンサに結像したときに波長がどれくらい空間的に離れているのか
を考えることは重要である。まず1つ目の波長変化dλに対する回折角度変化dβを求める。これを角分散と呼ぶが、
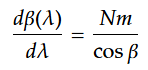
とあらわされる。そして、回折された光を焦点距離fのレンズでセンサに集光させると、f・dβ=dxとし両辺逆数をとると、
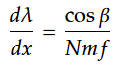
となる。これを逆線分散と呼ばれ、光学系の出口面上での単位長さあたりの波長差を意味する。これにスリット幅(1画素あたりの画素幅)を書けると波長分解の指標となる。
一方で、波長範囲はどうなるのか検討する。1次回折光で入射角度α、λ1からλ2をセンササイズdで受ける場合を考えると、
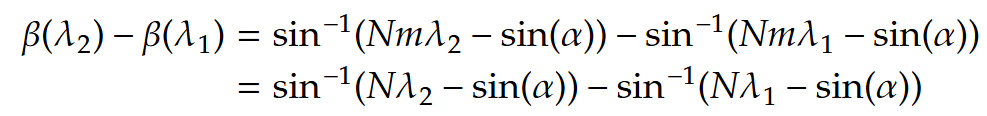
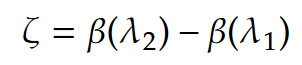
となっている。センサの必要なサイズはdは以下になる。
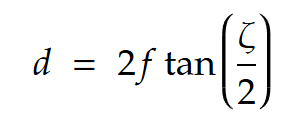



コメント