---

この節では、もう少し厳密にレーザの発振周波数に関して議論する。

前節までの議論を参考にすると共振器のモードωｍで発振するようなニュアンスで記載してきたが

実際はそう簡単でなく多少その周波数からずれていることをここでは示そう。

共振器内を伝搬するレーザ光は基本的にはエルミート・ガウスモード(電磁場節参照)である。

ｚ軸が変化することによる位相項は、伝搬モードが



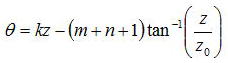
であった。共振器の両端のｚ値をｚ１とｚ２とすると、ｌ＝ｚ２－ｚ１でかつ、共振器長ｌの間に位相がｑπ変化したとすると



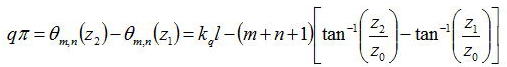
伝搬モード（ｍ、ｎ）＝（０，０）として、定常状態では共振器の往路と次の往路では位相のみしか変化していないことから



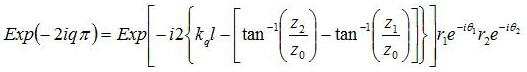
となる。ここで、ｒ１Exp（－ｉθ１）、、ｒ２Exp（－ｉθ２）はミラーによる反射によって振幅と位相が変調された量を表す。

ここで、波数ｋｑは電磁気の章で示したように



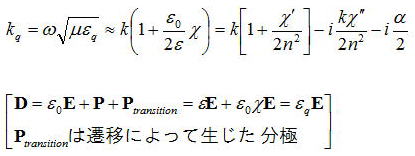
以前に述べたようにχ’’は遷移による吸収である。ここで言うαは遷移以外のすべての損失を意味している。

上記のｋｑを用いて位相項のみを抽出したときの方程式は、



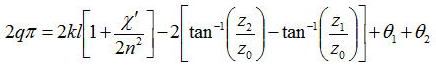
ここで、χ’＝０のときの周波数ω＝ωｑとして定義して以下のように記述できる。



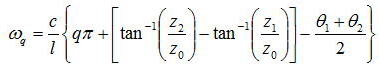
このωｑを用いて上記を整理しなおすと、



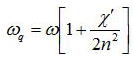
となる。この式はχ’は屈折率を意味しているが、発振周波数ωがレーザ媒質の屈折率により

ωｑからずれることを意味している。上式のχ’は周波数ωに依存するため、もう少しχ’を分解した形で表現したい。

ところで前節でレーザの発振条件に関して導いた。その発振条件で実数項と虚数項に分けてχ”/χ’を書き下すと



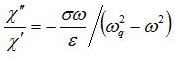
である。また次節で述べるが密度行列を用いた運動方程式から



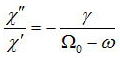
なので上式を整理すると、



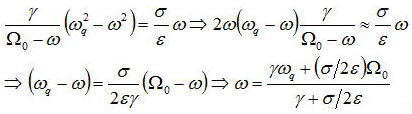
となる。上式が意味するところは、発振週亜h数が共振器モードωｑと原子の遷移周波数Ω０との

重みづけされた平均値になっている点である。実際、γとσ/２εではγの方が大きいのでほとんどωはωｑに近く

わずかにΩ０に引き込まれるだけである。このような現象を発振周波数の引き込みという。